基本介紹
- 中文名:生日攻擊
- 別稱:平方根攻擊
簡介,理解問題,數字簽名敏感度,另請參閱,
簡介
生日攻擊是一種密碼學攻擊手段,所利用的是機率論中生日問題的數學原理。這種攻擊手段可用於濫用兩個或多個集團之間的通信。此攻擊依賴於在隨機攻擊中的高碰撞機率和固定置換次數(鴿巢原理)。使用生日攻擊,攻擊者可在中找到散列函式碰撞,為原像抗性安全性。然而,量子計算機可在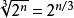 內進行生日攻擊(雖然飽受爭論)。
內進行生日攻擊(雖然飽受爭論)。
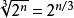
理解問題
主條目:生日問題
舉個例子,想像一位老師問一個有30名學生的班級(n = 30)每個人的生日在哪一天(為簡便,此處省略閏年)以確定是否有兩個學生同一天生日(對應碰撞 )。從直覺角度考慮,機率看起來很小。若老師選擇特定日期(例如9月16日),則至少有一名學生在那天出生的幾率是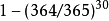 ,約為7.9%。但是,與我們的直覺相反的是,至少一名學生和另外任意一名學生有著相同生日的幾率大約為70.63%(n = 30時),從方程
,約為7.9%。但是,與我們的直覺相反的是,至少一名學生和另外任意一名學生有著相同生日的幾率大約為70.63%(n = 30時),從方程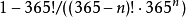 中可看出。
中可看出。
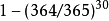
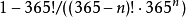
數字簽名敏感度
數位簽章可對生日攻擊十分敏感。構想一條被首次計算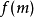 (f為密碼雜湊函式)所簽名的信息,且隨後又使用了一些密鑰來簽名
(f為密碼雜湊函式)所簽名的信息,且隨後又使用了一些密鑰來簽名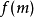 。假設愛麗絲與鮑伯牽涉到簽名詐欺契約。馬洛里準備了一份正常契約m和一份偽造契約m'。她隨後發現m所在的位置數可在不改變原意的情況下(如插入逗號、清空行、在句後增加一兩個空格、替換同義詞等等)被更改。通過結合這些更改,她可新建諸多m的變體且均為正常契約。
。假設愛麗絲與鮑伯牽涉到簽名詐欺契約。馬洛里準備了一份正常契約m和一份偽造契約m'。她隨後發現m所在的位置數可在不改變原意的情況下(如插入逗號、清空行、在句後增加一兩個空格、替換同義詞等等)被更改。通過結合這些更改,她可新建諸多m的變體且均為正常契約。
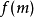
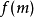
相似情況下,馬洛里也為偽造契約m'新建了諸多變體。她隨後套用哈希函式到所有變體直到她找到與正常契約有著相同哈希值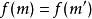 的偽造契約位置。她隨後將正常契約帶給鮑勃簽名。在鮑勃簽名完後,馬洛里將簽名取下並依附到偽造簽名上。此簽名“證實了”鮑勃簽署了偽造契約。
的偽造契約位置。她隨後將正常契約帶給鮑勃簽名。在鮑勃簽名完後,馬洛里將簽名取下並依附到偽造簽名上。此簽名“證實了”鮑勃簽署了偽造契約。
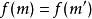
此例中,攻擊機率與原始的生日問題稍有不同,因為馬洛里將在尋找兩份具有相同哈希的正常契約與偽造契約時將一無所獲。馬洛里的策略是生成一份偽造和一份正常的契約。生日問題公式適用於n為契約對數的情況下。但馬洛里所生成的哈希數實際上為2n。
為避免這種攻擊,用於簽名方案的哈希函式的輸出長度應夠大以從計算角度防止生日攻擊。換言之,位數應為防止普通暴力破解所需位數的兩倍。
除了使用更大的位數長度外,簽名者(鮑勃)可以在簽名前做出一些隨機且無害的更改,並且在自己的手上留下一份契約副本以在法庭上展示出他的簽名與正常契約上的匹配,而不匹配偽造契約。
離散對數 Pollard Rho 算法是一項使用生日攻擊以計算離散對數的算法。
另請參閱
- 碰撞攻擊
