瑞利(Rayleigh)阻尼簡單、方便,因而在結構動力分析中得到了廣泛套用。瑞利(Rayleigh)阻尼假設結構的阻尼矩陣是質量矩陣和剛度矩陣的組合。結構的振型是關於質量矩陣和剛度矩陣正交的,很容易想到,質量矩陣和剛度矩陣的線性組合必定滿足正交條件,因此瑞利(Rayleigh)阻尼是一種正交阻尼。
基本介紹
- 中文名:瑞利阻尼
- 外文名:Rayleigh damping
- 定義:一種正交阻尼
- 套用學科:力學術語
- 範疇:數理科學
- 涉及:阻尼矩陣
概念,基本原理,特點,
概念
瑞利(Rayleigh)阻尼簡單、方便,因而在結構動力分析中得到了廣泛套用。瑞利(Rayleigh)阻尼假設結構的阻尼矩陣是質量矩陣和剛度矩陣的組合,即





結構的振型是關於質量矩陣和剛度矩陣正交的,很容易想到,質量矩陣和剛度矩陣的線性組合必定滿足正交條件,因此瑞利(Rayleigh)阻尼是一種正交阻尼。滿足振型正交條件的阻尼也稱為經典阻尼。在 式子中,
式子中, 和
和 是待定的兩個常數,可以用實際測量得到的結構阻尼比來確定(實測可直接給出結構的振型阻尼比),或通過給定的兩個振型阻尼比的值來確定,為此要把
是待定的兩個常數,可以用實際測量得到的結構阻尼比來確定(實測可直接給出結構的振型阻尼比),或通過給定的兩個振型阻尼比的值來確定,為此要把 式子化成由阻尼比表示的形式。
式子化成由阻尼比表示的形式。




基本原理
將 式子分別左乘振型的轉置
式子分別左乘振型的轉置 和右乘振型
和右乘振型 得
得











如果假設結構體系的阻尼滿足正交條件,並採用振型疊加法求解,則不必構造整體阻尼,而直接採用振型阻尼比 即可,因為實際結構阻尼測量中都是直接給出阻尼比。構造整體阻尼矩陣的目的是用於時域逐步積分分析,這時滿足正交條件的假設,或稱採用瑞利(Rayleigh)阻尼的目的,一是矩陣構造方便;而是用正交條件來確定係數
即可,因為實際結構阻尼測量中都是直接給出阻尼比。構造整體阻尼矩陣的目的是用於時域逐步積分分析,這時滿足正交條件的假設,或稱採用瑞利(Rayleigh)阻尼的目的,一是矩陣構造方便;而是用正交條件來確定係數 、
、 。
。



將公式 和
和 代入
代入 式子中,得:
式子中,得:




如果給定任意兩個振型阻尼比 (自振頻率是已知的),分別代入上式,即得到關於係數
(自振頻率是已知的),分別代入上式,即得到關於係數 和
和 的兩個線性代數方程組,可以解得
的兩個線性代數方程組,可以解得 和
和 ,則瑞利(Rayleigh)阻尼也就確定了,假設
,則瑞利(Rayleigh)阻尼也就確定了,假設 和
和 給定,可寫出計算
給定,可寫出計算 和
和 的矩陣形式
的矩陣形式















採用以上公式,經過簡單的運算就可以得到進行結構動力反應計算所需的阻尼矩陣。為保證構造的阻尼矩陣合理、可靠,在確定瑞利(Rayleigh)阻尼的常數 和
和 時,必須遵循一定的原則,否則構造的阻尼矩陣可能導致計算結果的嚴重失真。為此,下面分析瑞利(Rayleigh)阻尼的特點。
時,必須遵循一定的原則,否則構造的阻尼矩陣可能導致計算結果的嚴重失真。為此,下面分析瑞利(Rayleigh)阻尼的特點。


特點
將瑞利(Rayleigh)阻尼分成兩項,一項與質量矩陣成正比,一項與剛度矩陣成正比,即



相應地,阻尼比也分成兩項,與質量矩陣成正比項 和與剛度矩陣成正比項
和與剛度矩陣成正比項 ,即
,即





當常數 和
和 確定後,
確定後, 和
和 僅與
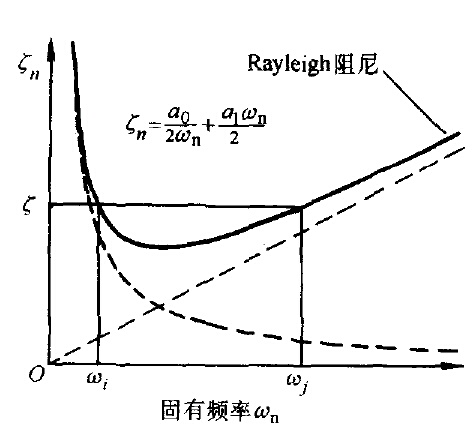
僅與 有關,圖1和圖2給出的阻尼比隨頻率
有關,圖1和圖2給出的阻尼比隨頻率 的變化規律曲線。
的變化規律曲線。






 圖1
圖1 圖2
圖2由圖1可見,與質量矩陣成正比的部分當頻率趨於零時,變得無窮大,隨著頻率的增加而迅速變小;與剛度矩陣成正比的部分,則隨著頻率的增加而線性增加。
由圖2可見,瑞利(Rayleigh)阻尼比 在兩個自振頻率
在兩個自振頻率 和
和 (用於確定瑞利阻尼常數的振型阻尼比對應的自振頻率)點處等於給定的阻尼比
(用於確定瑞利阻尼常數的振型阻尼比對應的自振頻率)點處等於給定的阻尼比 和
和 相等(這是工程中常用的,一般取各振型阻尼比均相同),則當振動頻率
相等(這是工程中常用的,一般取各振型阻尼比均相同),則當振動頻率 在
在 區間之內時,阻尼比將小於或等於給定阻尼比,而當頻率在這一區間之外時,其阻尼比均大於給定阻尼比,而且距離越遠,阻尼越大。
區間之內時,阻尼比將小於或等於給定阻尼比,而當頻率在這一區間之外時,其阻尼比均大於給定阻尼比,而且距離越遠,阻尼越大。







因此,確定瑞利阻尼的原則是:選擇的兩個用於確定常數 和
和 的頻率點
的頻率點 和
和 要覆蓋結構分析中感興趣的頻段。
要覆蓋結構分析中感興趣的頻段。




感興趣的頻率(頻段)的確定要根據作用於結構上的外荷載的頻率成分和結構的動力特性綜合考慮。
在頻段 內,阻尼比略小於給定的阻尼比
內,阻尼比略小於給定的阻尼比 (在
(在 ,
, 點有
點有 )。這樣,在該頻段內由於計算的阻尼略小於實際阻尼,結構的反應將略大於實際的反應,這樣的計算結果對工程而言是安全的。如果
)。這樣,在該頻段內由於計算的阻尼略小於實際阻尼,結構的反應將略大於實際的反應,這樣的計算結果對工程而言是安全的。如果 和
和 選擇的好,則可以保證這種增大程度很小。
選擇的好,則可以保證這種增大程度很小。







在頻段 以外,其阻尼比將迅速增大,這樣頻率成分的振動反應會被抑制,其計算值將遠遠小於實際值,但這一部分不是需要考慮的,或可以忽略的。但是,如果存在對結構設計有重要影響的頻率分量,則可能導致嚴重的不安全。
以外,其阻尼比將迅速增大,這樣頻率成分的振動反應會被抑制,其計算值將遠遠小於實際值,但這一部分不是需要考慮的,或可以忽略的。但是,如果存在對結構設計有重要影響的頻率分量,則可能導致嚴重的不安全。

因此,隨意找兩個自振頻率及相應阻尼比來確定 和
和 的方法是不對的,有可能導致嚴重的誤判。
的方法是不對的,有可能導致嚴重的誤判。