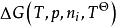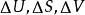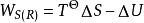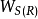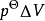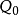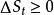基本介紹
- 中文名:理想功和損耗功
- 外文名:ideal work and lost work
- 記號:W(id)、W(L)
- 理想功條件:系統變化要在完全可逆條件下進行
- 損耗功特點:損耗功的值為非負值
- 套用領域:化工熱力學
定義,理想功,損耗功,穩定流動過程的理想功,計算公式,推導過程,注意事項,非流動過程的封閉系統理想功的計算,計算公式,推導過程,穩定流動過程的損耗功,計算公式,推導過程,注意事項,
定義
理想功
任何產功過程對於確定的狀態變化都存在一個最大功;任何耗功過程,對於確定的狀態變化都存在一個最小功。無論產功還是耗功過程,就功的代數值而言,都有一個最大值。此功在技術上可以利用,因此稱其為最大有用功,也稱為理想功,用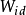 表示。
表示。
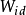
損耗功
損耗功的定義為系統在給定狀態變化過程中所提供的理想功與所做出的實際功差值,記作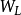 。
。
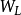
穩定流動過程的理想功
計算公式
已知
(2)狀態2:有溫度、壓力、焓與熵值分別為 的流體離開設備裝置。
的流體離開設備裝置。

則穩定流動過程的理想功計算式為:
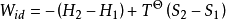
推導過程
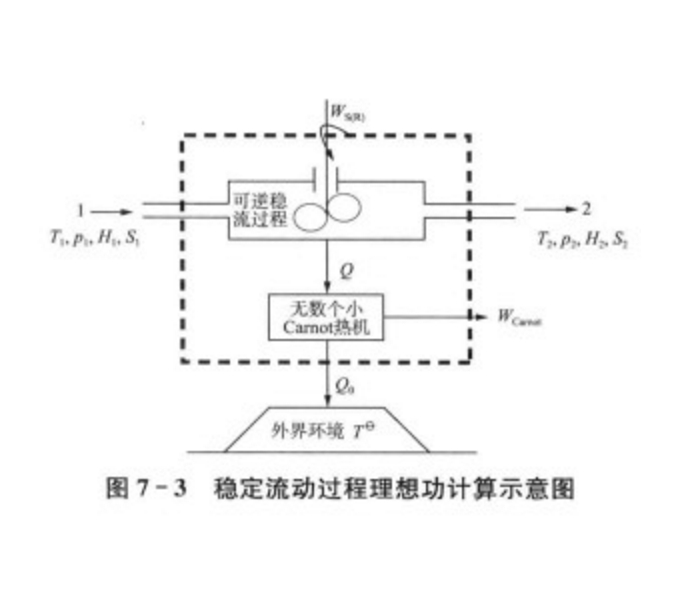
在穩定流動過程理想功計算的示意圖中,處於狀態1時,溫度、壓力、焓與熵值分別為 的流體進入設備裝置。在可逆穩定流動過程中,推動機器做可逆軸功
的流體進入設備裝置。在可逆穩定流動過程中,推動機器做可逆軸功 ,同時排出熱量Q;最後在狀態2,即流體的溫度、壓力、焓與熵值分別為
,同時排出熱量Q;最後在狀態2,即流體的溫度、壓力、焓與熵值分別為 的狀態下離開設備裝置。
的狀態下離開設備裝置。



為了對排出的熱量Q進行充分利用,設定Cornot熱機將部分熱量轉化為功,同時實現可逆傳熱。Cornot熱機做出的功稱為Cornot功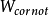 ,做功後,溫度下降到
,做功後,溫度下降到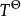 ,然後將溫度
,然後將溫度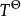 的熱量
的熱量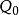 排到外界環境,外界環境就是Cornot熱機的低溫熱源。由於流體在穩定流動過程中是變溫的(由
排到外界環境,外界環境就是Cornot熱機的低溫熱源。由於流體在穩定流動過程中是變溫的(由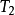 降到
降到 ),排出熱量Q時流體的溫度也是變化的,而Cornot熱機則要求恆溫熱源。為此可構想由無數個小Cornot熱機連續操作完成。每一個小Cornot熱機向高溫熱源吸收微量熱
),排出熱量Q時流體的溫度也是變化的,而Cornot熱機則要求恆溫熱源。為此可構想由無數個小Cornot熱機連續操作完成。每一個小Cornot熱機向高溫熱源吸收微量熱 ,做出微量Cornot功
,做出微量Cornot功 。因為小Cornot機的高溫源溫度變化極小,可以近似視為恆溫熱源。無數個Cornot機向高溫源吸收的總熱量為Q,它們所做總的Cornot功為
。因為小Cornot機的高溫源溫度變化極小,可以近似視為恆溫熱源。無數個Cornot機向高溫源吸收的總熱量為Q,它們所做總的Cornot功為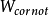 ,向外界環境排放總的熱量為
,向外界環境排放總的熱量為 。根據理想功的定義,在上述穩流過程中,理想功應是可逆軸功
。根據理想功的定義,在上述穩流過程中,理想功應是可逆軸功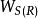 與Cornot功
與Cornot功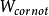 之和,即:
之和,即:
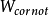
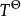
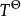
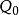
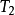



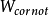

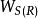
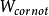

取包括Cornot機在內的設備裝置,根據敞開系統穩定流動過程的熱力學第二定律,即對於可逆過程,有:
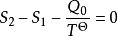
由此得:
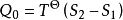
根據穩定流動過程的熱力學第一定律,可得:

綜合上式可得:
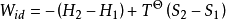
上式即為穩定流動過程的理想功計算式。
注意事項
(2)流體若是對外做功,則理想功為正值;反之,外界對流體做功,則理想功為負值。
(3)需要區分理想功與可逆軸功的概念與計算。有時可逆軸功是指無摩擦損耗的軸功,即流體在通過設備裝置時內部所有的變化都是可逆的,無任何損耗效應,此情況下提供的軸功即為可逆軸功。而要獲得理想功不僅要求設備裝置內部可逆,還要求外部可逆,即系統與環境的換熱也要可逆。這種情況只有藉助於Carnot熱機才能完成,所以理想功與可逆軸功之差值即為Carnot功。Carnot功可為正值也可為負值,因此理想功可大於也可小於可逆軸功。
(4)絕熱過程的Carnot功為零,因此絕熱過程的理想功與可逆軸功相等,理想功即為可逆軸功。
非流動過程的封閉系統理想功的計算
計算公式
已知:
(1)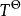 為周圍自然環境的溫度;
為周圍自然環境的溫度;
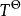
則非流動過程的封閉系統理想功的計算公式為:

推導過程
穩定流動過程的損耗功
計算公式
已知
(1)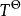 為周圍自然環境的溫度;
為周圍自然環境的溫度;
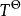
則在穩定流動過程中,損耗功的計算公式為:
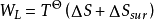

推導過程
已知系統在給定狀態變化過程中所提供的理想功為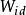 ,所做的實際功為
,所做的實際功為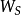 ,則在該穩定流動過程中,損耗功為:
,則在該穩定流動過程中,損耗功為:
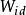
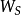

將理想功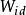 和實際功為
和實際功為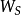 的計算公式代入上式,可得:
的計算公式代入上式,可得:
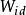
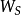


將上式代入到 中得:
中得:

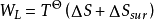
或者