球差

球差是由於電磁透鏡中心區域和邊緣區域對電磁波會聚能力不同而造成的。遠軸電磁波通過透鏡時被折射得比近軸電磁波要厲害得多，因而由同一物點散射的電磁波經過透鏡後不交在一點上，而是在透鏡相平面上變成了一個漫射圓斑。球差是限制透鏡分辨本領最主要的因素。

基本介紹

• 中文名：球差
• 外文名：Spherical aberration
• 領域：光學
• 別稱：球面像差
• 原因：中心和邊緣對電磁波會聚能力不同
• 相關名詞：慧差

簡介

軸上物點的物距L確定時，其像點位置L'是孔徑角U（或h）的函式，實際像點與理想像點的位置之差，叫做球差。球差（Spherical aberration）亦稱球面像差。軸上物點發出的光束，經光學系統以後，與光軸夾不同角度的光線交光軸於不同位置，因此，在像面上形成一個圓形彌散斑，這就是球差。一般是以實際光線在像方與光軸的交點相對於近軸光線與光軸交點（即高斯像點）的軸向距離來度量它。

對於單色光而言，球差是軸上點成像時唯一存在的像差。軸外點成像時，存在許多種像差，球差只是其中的一種。除特殊情況外，一般而言，單個球面透鏡不能校正球差，正透鏡產生負球差，負透鏡產生正球差。對一定位置的物點而言,當保持透鏡的孔徑和焦距不變時,球差的大小隨透鏡的形狀而異。因此，以適當形狀的正、負透鏡組合成的雙透鏡組或雙膠合鏡組是可能消球差的一種簡單結構。保持透鏡的焦距不變而改變透鏡形狀，猶如把柔軟的物體彎來彎去,故被稱為透鏡的整體彎曲,它是光學設計時校正像差的一種重要技巧。

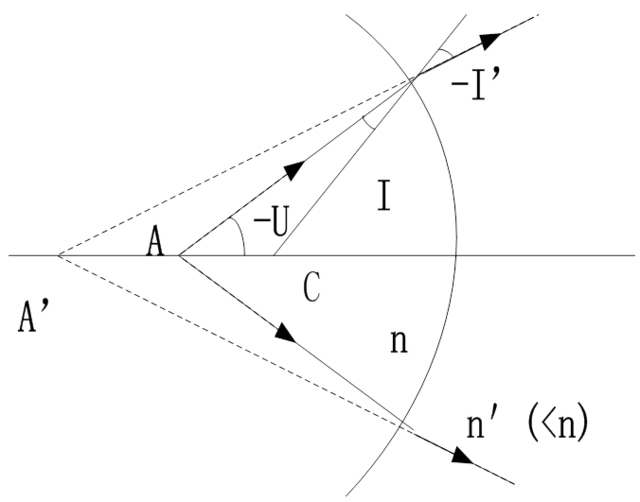
球差的形成原因

不同孔徑角U的光線交光軸於不同點上，相對於理想像點的位置有不同的偏離。

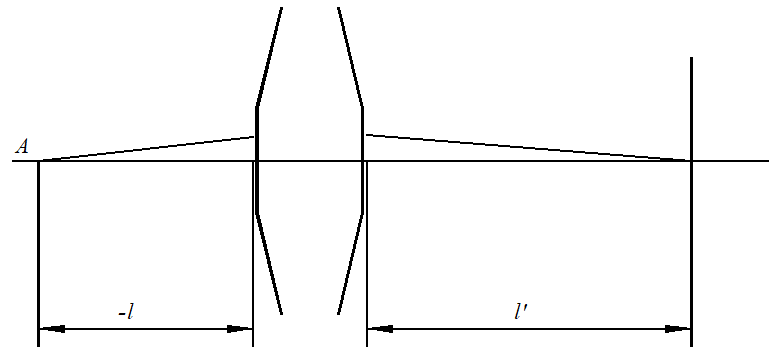
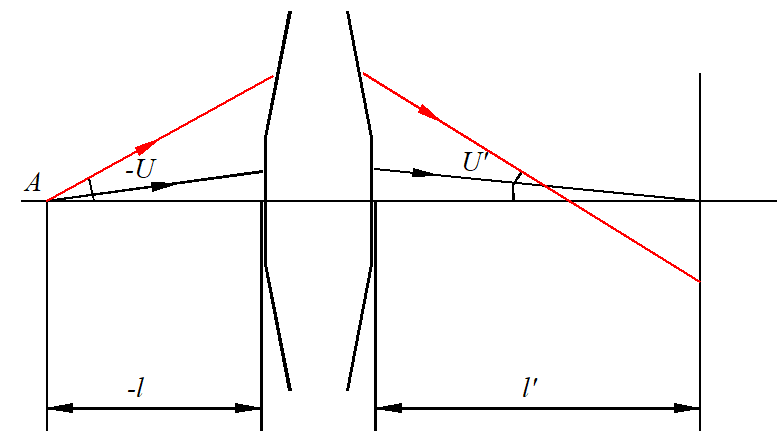
球差是軸上點唯一的單色像差。

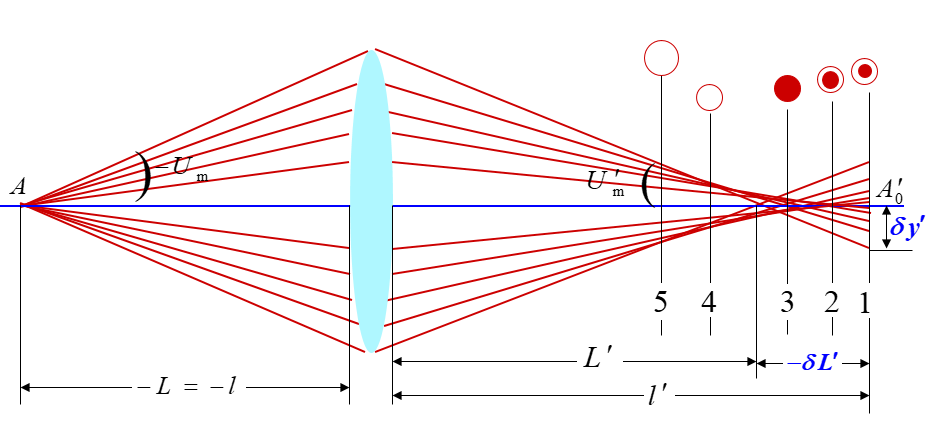
球差的度量

光束在高斯像面上並不是會聚於一個象點，而是一個圓形的彌散斑。

軸上球差：

垂軸球差：

符號規則：由理想像點計算到實際光線交點

dL>0 --- 正球差：

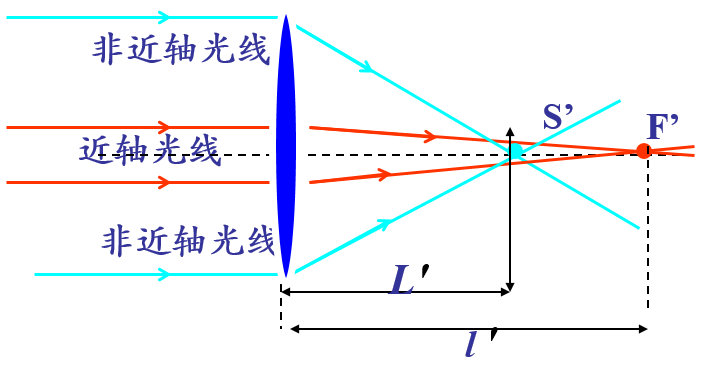
dL<0 --- 負球差：

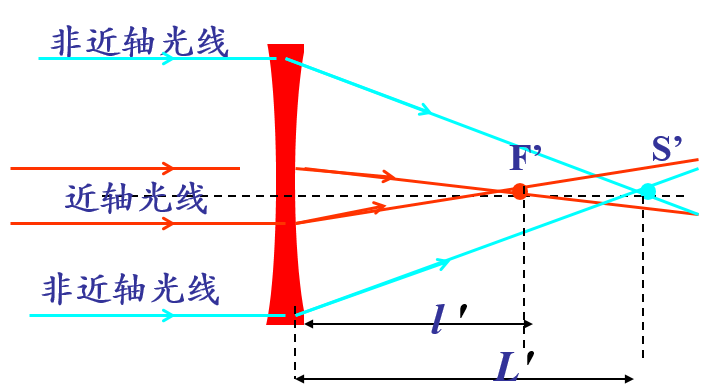
球差曲線

對應最大孔徑角U_max入射光線的高度h_max被稱為全孔徑（邊光球差）。

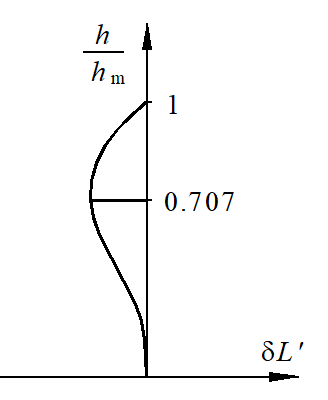
若，則稱為0.7孔徑或0.7帶光（帶光球差）。

球差校正不足

由於球差校正不足而產生如下形式的曲線：

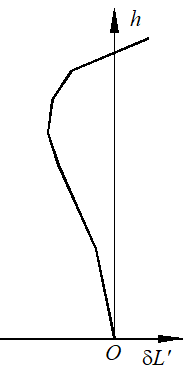球差過校正

球差過校正

由於球差過校正而產生如下形式的曲線：

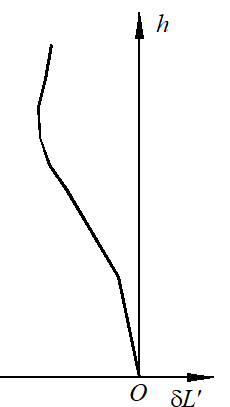球差校正不足

具有初級球差與二級球差時的另一種球差曲線

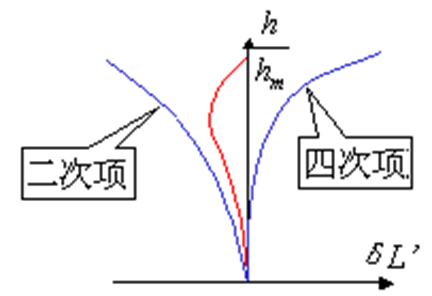
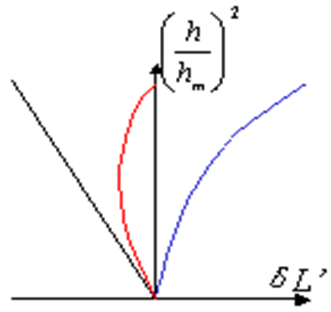
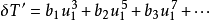
第一項稱為初級球差，後面各項依次稱為二級球差、三級球差等。初級球差以外的各項統稱為高級球差。

球差的影響

整個孔徑光束的垂軸球差在像面上形成了一個對稱於光軸的圓形彌散斑，嚴重時使軸上點成像變得模糊不清。

球差的校正

(1) 單個球面不產生球差的三個位置

(2) 齊明透鏡

(3) 單透鏡的球差

(4) 正負透鏡的組合

消球差

A、消球差系統一般只能使一個孔徑球差為零；

B、通常對邊緣孔徑校正球差；

C、不能使所有孔徑的球差為零；

D、負值球差—校正不足，正值球差—校正過頭。

球差分布公式

球差分布及表示

系統的總球差值是各個折射面產生的球差傳遞到象空間的疊加，每個折射面對球差均有貢獻，貢獻量值即為球差分布。

象方球差由兩部分組成：一為折射面本身產生的球差，二為物方球差乘以轉面倍率而得的球差。

象方球差：

轉面倍率：

球差分布係數與球差分布公式

球差分布係數：

折射面的與的乘積即為該折射面對光學系統總球差值的貢獻量。稱為球差係數。

球差分布係數的計算：

定義式：

計算式：，其中，。

運用

設單個折射球面的曲率半徑為r，兩邊媒質的折射率為n₁和n₂，則當物點處於三個位置，即球面頂點(物距u=0)、球心和由l=r+r*n₂/n₁所決定的點時，不產生球差，後二種情況有重要的套用。球面反射鏡僅當物點位於頂點和球心時無球差。

所有的迴轉二次非球面反射鏡，都有一對不產生球差的共軛點。其中，拋物面鏡是無窮遠軸上點和焦點；橢球面鏡和雙曲面鏡是它們的一對焦點。它們都有實際的套用。