狀態變數模型以數學的形式來表示一個系統的動態特性,包含狀態方程和輸出方程兩部分。狀態變數模型對於控制論的套用、複雜系統的處理都有很重要的意義,和工程系統相同,也套用於社會系統、經濟系統、生態學模型等系統的模型方面。狀態變數模型具有非唯一性。
基本介紹
- 中文名:狀態變數模型
- 外文名:State Variable Model
- 所屬範疇:內模型範疇
- 包含:狀態方程、輸出方程
- 意義:控制論的套用、複雜系統的處理
- 特性:具有非唯一性
簡介

基礎知識
狀態
狀態變數






狀態向量






狀態空間




狀態方程







輸出方程






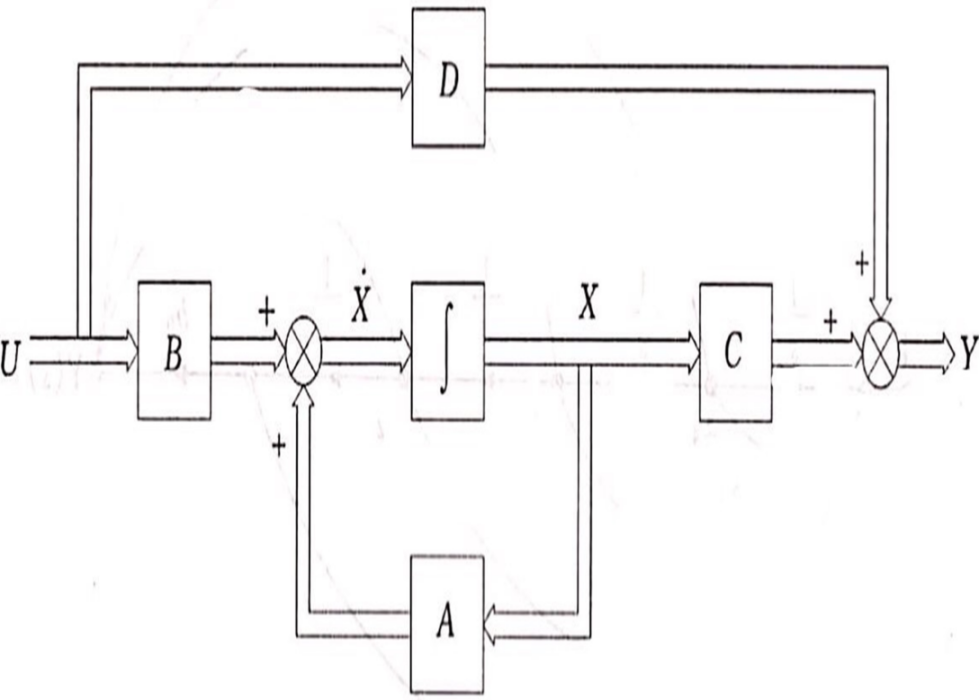
狀態變數模型以數學的形式來表示一個系統的動態特性,包含狀態方程和輸出方程兩部分。狀態變數模型對於控制論的套用、複雜系統的處理都有很重要的意義,和工程系統相同,也套用於社會系統、經濟系統、生態學模型等系統的模型方面。狀態變數模型具有非唯一性。






























為了達到某種加工目的,人們必須測量、建立和控制各種單元和過程系統的參變數。其中有些是人為設定的,如設備參數;有些是要調節控制的,如某些壓力、溫度和流量,稱為控制變數;有些是只測量而不控制的,稱為狀態變數。模型化是指把過程...
剪下強度相對較低和較大的高水平構造應力環境是煤岩系統滑移失穩的客觀條件,因此,可以用單狀態變數本構模型描述衝擊地壓的動力學行為。(2)粘滑是煤岩主要力學特性的一種表現形式,而衝擊地壓則是煤岩滿足剪下強度準則、以突然滑動並...
現代控制理論基礎課程共4個模組,包括狀態變數模型、狀態變數反饋控制系統設計、數字控制系統、非線性控制系統分析等內容。課程性質 課程定位 現代控制理論基礎課程是自動化類專業繼控制工程基礎之後的主要專業基礎理論課,是整個專業培養過程中...
1.1狀態變數和狀態變數模型 1.1.1狀態空間描述的基本概念 1.1.2狀態空間描述方法 1.2連續時間系統狀態空間表達式的建立方法 1.2.1通過物理機理建立狀態空間表達式 1.2.2通過微分方程建立狀態空間表達式 1.2.3通過傳遞函式建立狀態...
3.10利用MATLAB分析狀態變數模型 3.11循序漸進設計實例:磁碟驅動讀取系統 3.12小結 基礎練習題 一般練習題 難題 設計題 MATLAB練習題 術語和概念 第4章反饋控制系統的特性 ……第5章反饋控制系統的性能 第6章線性反饋系統的穩定性 ...
第6章線性控制系統的狀態空間分析 364 6.1引言 364 6.2線性定常系統的線性變換 364 6.2.1狀態變數模型的非唯一性 364 6.2.2狀態空間表達式的約當標準型 366 6.3線性定常系統的時間回響和狀態轉移矩陣 374 6.3.1齊次狀態方程...
第1章主要講述自動控制系統的一些基本概論;第2章為控制系統的數學模型;包括狀態變數模型;第3章為控制系統時域分析;第4章為線性系統的根軌跡技術;第5章為線性定常系統的頻域分析法;第6章為控制系統的校正設計;第7章為狀態變數...
第3章 狀態變數模型 第4章 反饋控制系統的特性 第5章 反饋控制系統的性能 第6章 線性反饋系統的穩定性 第7章 根軌跡方法 第8章 頻率回響法 第9章 頻域穩定性 第10章 反饋控制系統的設計 第11章 狀態變數反饋系統的設計 第12章...
10.3 線性狀態變數模型 317 10.4 分段線性模型 319 10.5 傳遞函式模型 324 10.6 非線性狀態變數模型 326 10.7 子系統 328 10.8 模型的死區時間 332 10.9 非線性車輛懸掛模型的仿真 334 10.10 控制系統和“硬體在迴路”測試...
第2章 線性控制系統的數學模型 2.1 基本知識點 2.1.1 數學模型 2.1.2 線性系統的微分方程 2.1.3 傳遞函式 2.1.4 結構圖 2.1.5 信號流圖 2.1.6 狀態變數模型 2.2 重點與難點 2.3 典型題解析 2.4 自我...
5.2.3期權定價Black—Scholes模型 5.3 差分方程建模 5.3.1 輸入一輸出問題(或狀態變數模型)5.3.2抵押貸款買房問題 5.3.3 減肥計畫安排問題 5.3.4連續模型的差分方法 5.3.5局部腦血流量的測定 5.4穩定性方法 5.4.1 ...
9.8 狀態變數模型 203 9.8.1 EMTDC/TCS接口實現 203 9.8.2 控制系統表示 205 9.9 小結 206 9.10 參考文獻 207 第10章 頻率相關網路等效 208 10.1 引言 208 10.2 FDNE的位置 209 10.3 降階系統的範圍 209 ...
從可壓縮瞬變流一維守恆形式的方程出發,通過引入空間位置交錯的兩種有限控制體積,提出了一維可壓縮瞬變流的有限元狀態變數模型,雖然稱為有限元模型,推導採用的方法在一維情況下也可稱為有限體積法,為拓寬模型的套用範圍,通過對能量...
