熱膨脹分析即是從測量金屬在溫度改變時或相變尺寸效應的變化來研究金屬內部的轉變,可以用來測定金屬在加熱與冷卻過程中的臨界點及熱膨脹係數等,並廣泛地用於研究鋼在淬火與回火狀態的各種變化。
基本介紹
- 中文名:熱膨脹分析
- 內容:研究金屬內部的轉變
- 要求:測定金屬在加熱與冷卻的臨界點
- 類型:物理
分析原理
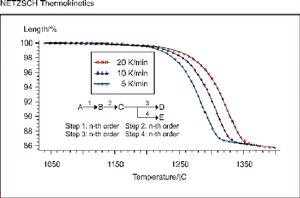
熱膨脹係數
嚴格說來,上式只是溫度變化範圍不大時的微分定義式的差分近似;準確定義要求ΔV與ΔT無限微小,這也意味著,

Vt=V0(1+3αΔT),
而對理想氣體,Vt=V0(1+0.00367ΔT);Vt、V0分別為物體末態和初態的體積。
對於可近似看做一維的物體,長度就是衡量其體積的決定因素,這時的熱膨脹係數可簡化定義為:單位溫度改變下長度的增加量與的原長度的比值,這就是線膨脹係數。
對於三維的具有各向異性的物質,有線膨脹係數和體膨脹係數之分。如石墨結構具有顯著的各向異性,因而石墨纖維線膨脹係數也呈現出各向異性,表現為平行於層面方向的熱膨脹係數遠小於垂直於層面方向。
巨觀熱膨脹係數與各軸向膨脹係數的關係式有多個,普遍認可的有Mrozowski算式:α=Aαc+(1-A)αa
αc,αa分別為a軸和c軸方向的熱膨脹率,A被稱為“結構端面”參數。
分析對象

固體熱膨脹:固體熱膨脹現象,從微觀的觀點來分析,它是由於固體中相鄰粒子間的平均距離隨溫度的升高而增大引起的。晶體中兩相鄰粒子間的勢能是它們中心距離的函式,根據這種函式關係所描繪的曲線,如圖2-6所示,稱為勢能曲線。它是一條非對稱曲線。在一定溫度下,粒子在平衡位置附近振動、具有的動能為EK,總能量為EK與相互作用能EP之和,它在整個運動過程中是守恆的。圖中,粒子間最接近的距離是r′,最遠的距離是r〃。由於距離減小所引起的斥力增長比由於距離增大所引起的引力下降快的多,因而粒子間接近的距離與粒子間遠離的距離關係是 r0r′<r〃-r0所以兩相鄰粒子中心的平均距離為 變的情形。由此可見,當晶體溫度升高,粒子熱振動加劇,體積膨脹。
固體的線膨脹:由於固體隨溫度的變化而變化,當溫度變化不太大時,在某一方向長度的改變數稱為“固體的線膨脹”。例如,一細金屬棒受熱而伸長。固體的任何線度,例如,長度、寬度、厚度或直徑等,凡受溫度影響而變化的,都稱之為“線膨脹”。
線膨脹係數:亦稱線脹係數。固體物質的溫度每改變1攝氏度時,其長度的變化和它在0℃時長度之比,叫做“線膨脹係數”。單位為1/開。符號為αl。其定義式是 即有lt=l0(l+αlt)。由於物質的不同,線膨脹係數亦不相同,其數值也與實際溫度和確定長度l時所選定的參考溫度有關,但由於固體的線膨脹係數變化不大,通常可忽略這種變化,而將α當作與溫度無關的常數。
固體的面膨脹:當固體的溫度變化不大時,其表面積隨溫度的升高而增大,這一現象叫“固體的面膨脹”。遵循的規律為:St=S0(1+αst)式中αs為面膨脹係數,單位是1/開,其量值為αs≈2ατ。
固體的體膨脹:當固體的溫度變化不大時,其體積隨溫度的升高而增大,這一現象叫“固體的體膨脹”。

體積膨脹係數:或稱“體脹係數”。無論物質是哪種(固體、液體或氣體)形態的變化,都稱之為體膨脹。當物體溫度改變1攝氏度時,其體積的變化和它在0℃時體積之比,叫做“體積膨脹係數”。符號用α表示。設在0℃時物質的體積為V0,在t℃時的體積為Vt,則體脹係數的定義式為 即有Vt=V0(1+αt)。由於固體或液體的膨脹係數很小,為計算方便起見,在溫度不甚高時,可直接用下式計算,無需再求0℃時的體積V0V2=V1[1+α(t2-t1)]。式中V1是在t1℃時的體積,V2是在t2℃時的體積。這一式只適用於固體或液體,因為氣體物質的膨脹係數值較大,不能運用此式。
液體熱膨脹:液體是流體,因而只有一定的體積,而沒有一定的形狀。它的體膨脹遵循Vt=V0(1+βt)的規律,β是液體的體膨脹係數。其膨脹係數,一般情況是比固體大得多。
氣體的熱膨脹:氣體熱膨脹的規律較複雜,當一定質量氣體的體積,受溫度影響上升變化時,它的壓強也可能發生變化。若保持壓強不變,則一定質量的氣體,必然遵循著Vt=V0(1+γt)的規律,式中的γ是氣體的體膨脹係數。蓋·呂薩克定律,反映了氣體體積隨溫度變化的規律。這一定律也可表述為:一定質量的氣體,在壓強不變的情況下,溫度每升高(或降低)1℃,增加(或減小)的體積等於它在0℃時體積。
