無窮遠奇點是平面奇點的一種推廣,用於研究平面系統的軌線在平面上無窮遠處的性態。
基本介紹
- 中文名:無窮遠奇點
- 外文名:critical point at infinity
- 適用範圍:數理科學
簡介
龐加萊球面

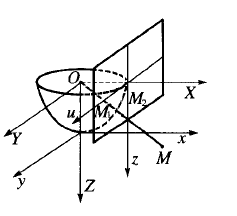 圖1
圖1



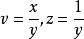

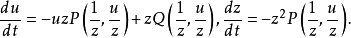


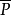
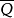

意義


無窮遠奇點是平面奇點的一種推廣,用於研究平面系統的軌線在平面上無窮遠處的性態。

 圖1
圖1



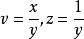

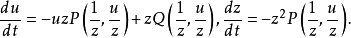


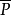



無窮遠奇點是平面奇點的一種推廣,用於研究平面系統的軌線在平面上無窮遠處的性態。...... 無窮遠奇點是平面奇點的一種推廣,用於研究平面系統的軌線在平面上無窮遠...
在奇點宇宙沒有空間,宇宙半徑尺趨近於零。奇點是一個密度無限大,熱量無限大,溫度無限高,壓力無限大,時空曲率無限大,體積無限小的“點”。在奇點宇宙處於高密高溫...
一個代數集合在(x,y)維度系統定義為y= 1/x有一奇點(0,0),因為在此它不允許切線存在。[1] 幾何學中的奇點 “幾何意義上的奇點”,也是無限小且不實際存...
物理上把一個存在又不存在的點稱為奇點,空間和時間具有無限曲率的一點,空間和時間在該處完結。經典廣義相對論預言奇點將會發生,但由於理論在該處失效,所以不能...
物理上把一個存在又不存在的點稱為奇點。空間和時間具有無限曲率的一點,空間和時間在該處完結。經典廣義相對論預言奇點將會發生。在具有合理物質源的廣義相對論的...
奇點分布法是解無粘性不可壓縮流體無旋運動的問題的一個重要方法。無粘性不可...式中Vˉ∞、Q、Γ分別為無窮遠處共軛速度、點源強度、速度環量;Μ=meiβ為...
1 臨界半徑 2 無限紅移面 偽奇點臨界半徑 編輯 對於一個球對稱的靜態引力場,其時空幾何是Schwarzshild幾何,其時空間隔(解)為:根據觀察,我們看到當 r 趨近於2GM...
第六章 無窮遠奇點與全局結構 6.1 無窮遠奇點 6.2 軌線的全局結構分析舉例 習題6 第七章 高維系統的奇點分析 7.1 線性系統的奇點 7.2 穩定流形...
亞純函式的極點是一種特殊的奇點,它的表現如同 時 的奇點。這就是說,如果當z趨於a時,函式 趨於無窮大,那么 在z=a處便具有極點。...
研究攝動量級數解中共振奇點的理論。這種共振奇點的問題與一般力學中的共振現象...但這隻意味著級數解失效﹐絕對不能說明軌道要素真的會變為無窮大。運動方程本身...
