偽奇點

臨界半徑

對於一個球對稱的靜態引力場，其時空幾何是Schwarzshild幾何，其時空間隔(解)為：

根據觀察，我們看到當 r 趨近於2GM時，這一時空間隔出現一個“奇點”。在這一半徑處，

g00=1 - 2GM/r 趨於 0 ················································· (1)

且

g11= - 1/（2GM/r)趨於無窮············································(2)，

在cgs單位制中，臨界半徑為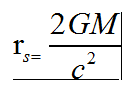

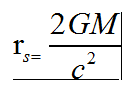
這稱為Schwarzshild半徑，或者質量M的引力半徑。對於一個M=2*10的三次方g的質量，這一半徑為rs=3.0km。

* 如果一個天體的實際半徑大於rs，則我們不需要考慮奇點（1）、（2）式，因為Schwarzshild解只適用於該天體的外部區域。

* 如果一個天體具有小於rs的半徑，它必然具有~10的16次方g/cm立方的密度，這一密度甚至比中子星的密度還要大。

注意，天體的大小小於Schwarzshild半徑時，其相應的臨界密度隨質量的增大而減小。

為討論Schwarzshild解的普遍特徵，假設天體已經完全坍縮，因而在所有的點，質量密度都為0（r=0點除外）。這表明可以把Schwarzshild解當做Einstein方程一個嚴格真空解來處理

r=rs（看作是時空中的一個曲面）對應的曲面稱為無限紅移面（史瓦西解的情況下重合事件視界）。一隻鄰近r=rs的靜止鐘，其故有時為

當r=rs時它趨於零；即，比起另一隻位於無限遠處的鐘，這隻鐘走得無限慢。這樣，如果一個靜止於接近r=rs處的太空人向外傳送光脈衝或是信號火箭，其相繼脈衝之間的時間間隔為1s(在他的時鐘看來)，則遠距離處的觀測者將以遠大於1s的時間間隔接收到這些脈衝。

對於一隻位於r=rs處的靜止鐘，上式給出了一個無限大的時間膨脹。事實上，鐘不可能在這個面上保持靜止。

r=rs處的Schwarzshild “奇點”不是一個物理的點。（1）（2）中的奇點是“偽奇點”，它的出現是由於不適當的坐標選擇，並可以經過坐標變換而消失。