無窮可分律(infinitely divisible la w)是一類機率分布律。
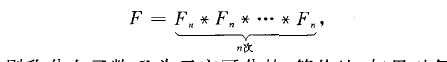


無窮可分律(infinitely divisible la w)是一類機率分布律。
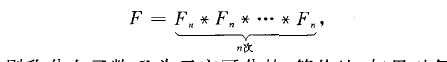


無窮可分律(infinitely divisible la w)是一類機率分布律。...... 無窮可分律(infinitely divisible la w)是一類機率分布律。如果對每個正整數,,都存在分布函式F...
李增滬證明斜卷積半群與無窮可分機率進入律之間的1-1對應關係,並在此後的論文中發展了相應的移民超過程理論。斜卷積半群作為開放系統的研究工具也適用於若干其它...
重對數律,不變原理,無窮可分律的理論及其套用等;三、隨機過程論,包括可數狀態離散時間的馬爾可夫鏈,可數狀態連續時間的馬爾可夫過程,隨機環境中馬爾可夫鏈,鞅論等...
了逆轉公式和連續性定理,他將古典中心極限定理收斂於正態律的提法改變為收斂於穩定律,他提出(而為Α.Я.辛欽所證明)無窮小三角序列的極限律類為無窮可分分律類...
1949年,格涅堅科和柯爾莫哥洛夫發表了專著《相互獨立隨機變數之和的極限分布》,這是一部論述20世紀30年代以來,柯爾莫哥洛夫和辛欽等以無窮可分律和穩定律為中心...
柯爾莫哥洛夫(Колмогоров)建立機率論的公理體系為標誌,蘇聯在這一領域取得了無可爭辯的領先地位.近代極限理論——無窮可分分布律的研究也經C.H....
近代極限理論——無窮可分分布律的研究也經C.H.伯恩斯坦(Бернштейн)、A.Я.辛欽(Хинчин)等人之手而臻於完善,成為切比雪夫所開拓的古典極限...
他的代表性研究成果分三個方面。(1) 李增滬提出了斜卷積半群的概念,以此給出了測度值移民過程的公理化定義形式。他建立了斜卷積半群與無窮可分進入律之間的1-1...
穩定分布是一類無窮可分分布,稱隨機變數X的機率分布為穩定的,如果對於任意實數a1>0,a2>0,b1和b2,存在實數a>0和b,使其分布函式F(x)滿足條件:F(a1x+b1)*...
1932年得到了含二階矩的隨機變數具有無窮可分分布律的充要條件。1933年出版了《機率論基礎》一書,在世界上首次以測度論和積分論為基礎建立了機率論公理結論,這是...
他證明了:①作為強大數律先聲的辛欽弱大數律;②隨機變數的無窮小三角列的極限分布類與無窮可分分布類相同。還研究了分布律的算術問題和大偏差極限問題。 他對...
他首先與柯爾莫哥洛夫討論了隨機變數級數的收斂性,他證明了:(1)作為強大數律先聲的辛欽弱大數律;(2)隨機變數的無窮小三角列的極限分布類與無窮可分分布類相同...
