若不等式的不等號兩邊都是代數式，並且其中至少有一個是代數無理式，則稱這樣的不等式為無理不等式(irrational inequality)，或根式不等式，無理不等式常常轉化為等價有理不等式(組)來求解。
基本介紹
- 中文名：無理不等式
- 外文名：irrational inequality
- 別稱：根式不等式
- 所屬學科：數學（代數）
- 簡介：含有無理式的代數不等式
基本介紹,例題解析,
基本介紹
1.確定未知數的允許值範圍。
3.求解不等式(組)。
4.取不等式(組)的解集與未知數允許值範圍的公共部分。在化去根式時，常依據的同解定理有：
f(x)<g(x)
[f(x)]<[g(x)](k∈N+)；
或設f(x)≥0，g(x)≥0，k∈N+時，則
f(x)<g(x) [f(x)]<[g(x)].
解無理不等式的關鍵是將無理不等式轉化為有理不等式，在轉化過程中，常常通過乘方的方法去掉根號，對於含有偶次根式的不等式，既要使各個根式都有意義，又要在進行偶次乘方時保證不等式兩邊的作負性，才能使變形保持同解。
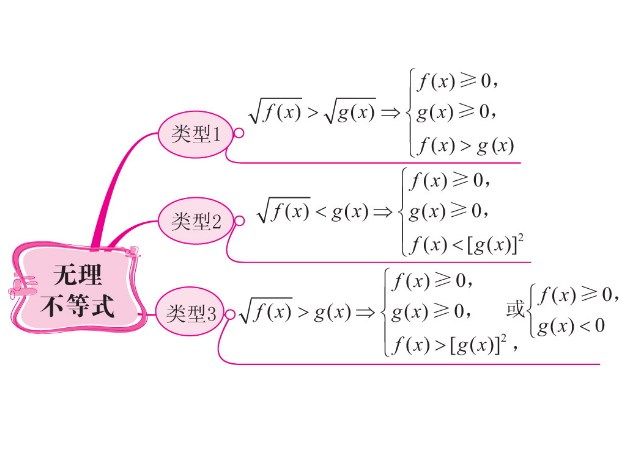
含二次根式的無理不等式的解法，關鍵是把它同解變形為有理不等式(組)，其基本變形有：
例題解析
在被開方式中含有未知數的不等式叫無理不等式，無理不等式解法的主要思想是利用不等式乘方性質，去掉根號化為有理不等式和直接利用算術根的定義來解。
【例1】解下列不等式
解 解原不等式等價於解下列不等式組
說明：一定要注意含有一個二次根式的無理不等式兩種基本類型解法的區別，產生這種區別的原因在於
類型，根據算術根的意義，當f2(x) <0時，原不等式不可能成立，故此時無解。而
