無反射邊界條件,是一種在計算中出現的特殊情況。新的有界區域上的解應是原來的無界區域上解的好的近似。對波動方程來說,這就要求在人工邊界上不產生人工(非物理)反射。因而這類邊界條件稱為無反射邊界條件或吸收邊界條件
基本介紹
- 中文名:無反射邊界條件
- 外文名:nonreflecting boundary condition
- 學科:數理科學
- 類型:力學術語
- 特點:計算中出現的特殊情況
- 邊界條件:運動邊界上方程組解應滿足的條件
簡介,邊界條件,相關研究,數值模擬,
簡介
在科學和工程計算中,大量出現無界或半無界區域上各種波動方程的數值求解問題,由於計算機容量有限,一般只能在有界區域上計算,為此需引進人工邊界,在這些邊界止應加相應的邊界條件。這些邊界條件應滿足兩個基本要求:
1)新的有界區域上的解應是原來的無界區域上解的好的近似。對波動方程來說,這就要求在人工邊界上不產生人工(非物理)反射。因而這類邊界條件稱為無反射邊界條件或吸收邊界條件;
2)所形成的微分方程初邊值問題是適定的。
邊界條件
邊界條件指在運動邊界上方程組的解應該滿足的條件。有限元計算,無論是ansys,abaqus,msc還是comsol等,歸結為一句話就是解微分方程。而解微分方程要有定解,就一定要引入條件, 這些附加條件稱為定解條件。定解條件的形式很多,最常見的有兩種——初始條件和邊界條件。
如果方程要求未知量y(x)及其導數y′(x)在自變數的同一點x=x0取給定的值,即y(x0)=y0,y′(x0)= y0′,則這種條件就稱為初始條件,由方程和初始條件構成的問題就稱為初值問題;
而在許多實際問題中,往往要求微分方程的解在在某個給定區間a ≤ x ≤b的端點滿足一定的條件,如y(a) = A , y(b) = B,則給出的在端點(邊界點)的值的條件,稱為邊界條件,微分方程和邊界條件構成數學模型就稱為邊值問題。
相關研究
近年來在計算氣動聲學(Computational Aero-Acoustics,CAA)中提出了將大渦模擬和聲學傳播方程相結合的計算聲場的混合方法。這種混合方法的思路是將聲場的計算區域分成聲源區域和傳播區域,在聲源區域採用大渦模擬方法,在傳播區域採用求解聲學傳播方程。該方法由於避免了全場採用大渦模擬等直接方法進行模擬,因此大大減少了計算時間,近年來成為計算氣動聲學的研究熱點。其中大渦模擬區域基於計算量的考慮,不能取得很大,這就涉及到一個邊界條件的處理問題。遠場邊界條件的處理非常重要,若處理不當,將在邊界上產生較大反射“污染”計算區域的流場,影響計算精度。
作為大渦模擬的前期工作,陳榮錢等研究了採用有限差分法求解二維Navier- Stokes方程的遠場邊界處理問題。遠場邊界條件通常採用特徵無反射邊界條件。特徵無反射邊界條件最早是由Thompson提出,套用在笛卡爾格線下歐拉方程的計算中;Pointsot將其套用到笛卡爾格線的可壓縮Navier- Stokes方程的計算中;蔣莉將特徵無反射邊界條件推廣到一般曲線坐標系下可壓縮N-S方程的計算中,在邊界上控制方程改寫成原始變數的形式,出口邊界採用了鬆弛因子的方法減小出口反射;Kim提出了另一種一般曲線坐標系下的特徵邊界條件處理方法,但在邊界上控制方程寫成守恆變數的形式,同時在入口邊界和出口邊界都採用了鬆弛因子方法。最近五年,Yoo認為局部一維無粘關係式中省略的橫向對流項及粘性項應當保留;Chen給出了新的一般曲線坐標系下的特徵邊界條件的數學推導,並將邊界條件和採用隱式時間推進求解的內場禍合起來;Landmann將一般曲線坐標系下特徵反射和無反射邊界條件寫成統一的公式,給出了數學推導。由此可以看出,特徵無反射邊界條件雖然經歷了二十多年的發展,取得了一系列的成果,但直到目前仍然是一個需要研究的問題。
數值模擬
正確處理可壓縮流動的邊界條件是得到直接數值模擬結果非常關鍵的一步,因為在直接數值模擬中不可能模擬一個無限大的計算區域.由於計算資源的限制,常會人為地將直接數值模擬的計算區域限制在一個非常有限的區域內,這樣就只能在有限的計算區域內給定特定的邊界條件口。
對於Navier-Stokes方程的特徵邊界條件的給定,目前學術界尚存在很大爭議。主要的問題集中在Navier-Stokes不是雙曲型方程,因此不能簡單將Eider方程邊界條件給定的方法直接套用到Navier-Stokes方程,但是,對於Navier-Stokes方程,存在類似於Eider方程傳播的特徵波,為了處理Navier-Stokes方程的特徵邊界條件,先假定Navier-Stokes傳播的特徵波主要是Eider方程中特徵波的部分,至於Navier-Stokes特徵波的詳細形式需要在今後數學理論發展之後再進行詳細考慮。目前,學術界正是在上述假定下採用類似於Eider特徵波分析的方法來處理Navier-Stokes方程的特徵波。
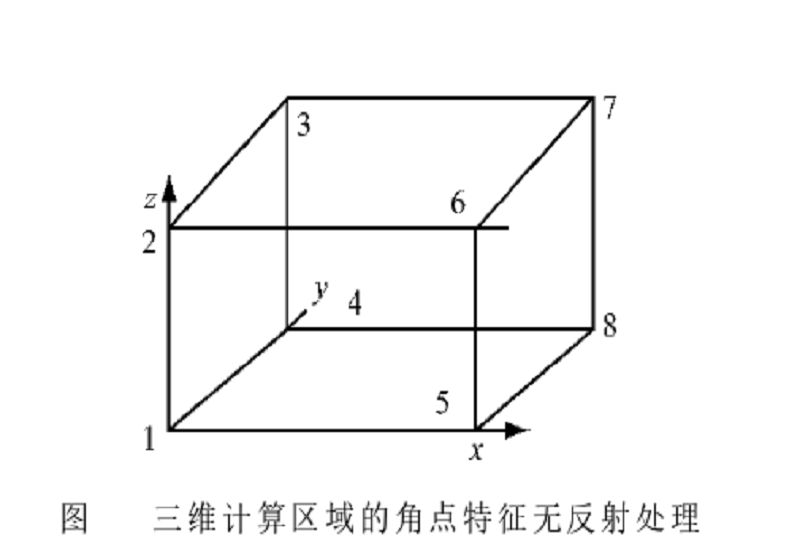
李德波等對特徵無反射邊界條件中角點的邊界條件處理進行了研究,並通過大量的數值模擬,提出了新的角點耦合處理數學方法。與此同時,對空間發展的可壓縮圓孔射流進行了直接數值模擬研究,並將模擬結果與試驗值進行了嚴格驗證,結果發現直接數值模擬結果與試驗值吻合較好,表明新的角點耦合處理數學方法是有效的。