基本介紹
- 中文名:濃度三角
- 別稱:十字交叉法
- 套用學科:數學
- 適用領域範圍:濃度糖水混合
公式,濃度表示方法,套用與推廣,例題,簡化的方法,靈活的技巧,廣泛的套用,總結,
公式
濃度=溶質/(溶劑+溶質)
濃度指某物種在總量中所占的分量。
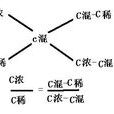
把混合的兩種物質並排寫在一張紙上,把他們的濃度和質量寫在他們旁邊,把混合後的物質寫在那兩個物質的中間的下方,這樣三種物質形成了一個倒三角形。比如說進行混合的兩物質是A和B,濃度分別是m和n,質量分別是x和y,混合後的物質是C,濃度是p,質量是z。那么滿足如下關係:z=x+y p-m:n-p=y:x。所以m,n,p,x,y,z這六個量只要知道4個其他兩個就可以求出了。
濃度表示方法
重量百分濃度:一般使用最常用。
體積百分濃度:常用於酒類表示。
體積摩爾濃度:化學常用。
重量摩爾濃度
套用與推廣
初看題目,有人說,濃度問題是百分數套用題中較複雜的內容,涉及溶質、溶劑、溶液的關係,另外還有“稀釋”、“蒸發”、“多種溶液混合”等各種變化,做起來已經很亂了,為什麼還提倡將其他問題轉化成濃度問題來解答呢?先請大家帶著這個問題來看幾道例題。
例題
簡化的方法
簡化了的方法更容易被人接受和利用。我們先通過幾道簡單的問題了解一下新的方法。
例1有濃度為20%的鹽水300克,要配製成40%的鹽水,需加入濃度為70%的鹽水多少克?
解析 1.將兩種溶液的濃度分別放在左右兩側,重量放在旁邊,配製後溶液的濃度放在正下方,用直線相連;與十字交叉法類似
2.直線兩側標著兩個濃度的差,並化成簡單的整數比。所需溶液的重量比就是濃度差的反比;
3.對“比”的理解應上升到“份”,3份對應的為300克,自然知道2份為200克了。
答:需加入濃度為70%的鹽水200克。
例2將75%的酒精溶液32克稀釋成濃度為40%的稀酒精,需加入水多少克?
解析 稀釋時加入的水溶液濃度為0%(如果需要加入乾物質,濃度為100%),標註數值的方法與例1相同。(見圖2)
32÷8×7=28
答:需加水28克。
例3買來蘑菇10千克,含水量為99%,晾曬一會兒後,含水量為98%,問蒸發掉多少水份?
解析 做蒸發的題目,要改變思考角度,本題就應該考慮成“98%的乾蘑菇加水後得到99%的濕蘑菇”,這樣求出加入多少水份即為蒸發掉的水份,就又轉變成“混合配比”的問題了。但要注意,10千克的標註應該是含水量為99%的重量。將10千克按(99%-98%):(100%-99%)分配,
答:蒸發掉5千克水份。
靈活的技巧
“解題有法,但無定法”,解題方法的運用要講究技巧,根據具體題目加以靈活運用,不要生搬硬套,形成定式。
例4甲容器中有純酒精11升,乙容器中有水15升,第一次將甲容器中的一部分純酒精倒入乙容器,使酒精與水混合。第二次將乙容器中的混合液倒入甲容器。這樣甲容器中純酒精含量為62.5%,乙容器中純酒精的含量為40%。那么第二次從乙容器中倒入甲容器的混合液是多少升?
解析 1、乙中酒精含量為40%,是由若干升純酒精(100%)和15升水混合而成,可以求出倒入乙多少升純酒精。15÷3×2=10升
62.5%,是由甲中剩下的純酒精11-10=1升,與40%的乙混合而成,可以求出第二次乙倒入甲多少升.
廣泛的套用
通過前面例題的講解,我們發現,新的解法利用濃度差的比與重量的比成反比的關係,把題目退到“份數”上考慮,數據也變簡化了。這種方法套用較廣泛,有些題目適合用這種方法解答。
例5某班有學生48人,女生占全班的37.5%,後來又轉來女生若干人,這時人數恰好是占全班人數的40%,問轉來幾名女生?
濃度差之比1∶24 48÷24×1=2人
重量之比 24∶1
解析 這是一道變換單位“1”的分數套用題,需抓住男生人數這個不變數,如果按濃度問題做,就簡單多了。
答:轉來2名女生。
例6服裝廠出售6000件男女服裝,男式皮衣件數占男衣的12.5%,女
裝中男式皮衣有多少件?女式皮衣有多少件?
解析 可以把皮衣件數占服裝的百分比理解成濃度,畫出分析圖:(見圖6)
答:男式皮衣有300件,女式皮衣有900件。
例7甲乙兩個倉庫共存放420噸貨物,甲倉運出的貨物相當於餘下貨物
甲倉原有貨物多少噸?乙倉原有貨物多少噸?
解析 這題中兩個分率出現有些特殊,單位“1”為餘下貨物,為了運用濃度問題進行計算,需將單位“1”轉化為全部物品。這樣甲運走了它的
再根據濃度配比計算。
答:甲倉原有貨物180噸,乙倉原有貨物240噸。
例8小明到商店買紅、黑兩種筆共66支。紅筆每支定價5元,黑筆每支定價9元。由於買的數量較多,商店就給予優惠,紅筆按定價85%付錢,黑筆按定價80%付錢,如果他付的錢比按定價少付了18%,那么他買了紅筆多少支?
(北京市第14屆迎春杯數學競賽初賽試題)
解析 紅筆按85%優惠,黑筆按80%優惠,結果少付18%,相當於按82%優惠,可按濃度問題進行配比。與其他題不同的地方在於紅、黑兩種筆的單價不同,要把這個因素考慮進去。然後就可以按比例分配這66支筆了。
答:他買了36支紅筆。
總結
通過以上例題,我們可以看出,只要我們在解題時善於抓住事物間的聯繫,進行適當轉化,就能發現其中的規律,找到解決問題的巧妙方法。