與一條曲線C的所有切線相交成直角的曲線Γ,稱為曲線C的漸開線(evolent)。一般的漸開線指“圓的漸開線”。在平面上,一條動直線(發生線)沿著一個固定的圓(基圓)作滾動的過程中,此直線上任意一點的軌跡,稱為此基圓的一條漸開線。
基本介紹
- 中文名:漸開線、漸伸線、漸屈線
- 外文名:evolent
- 學科:數學、機械工程
- 廣義釋義:與曲線所有切線相交成直角的曲線
- 狹義指:圓的漸開線
- 性質:基圓以內無漸開線,等
定義
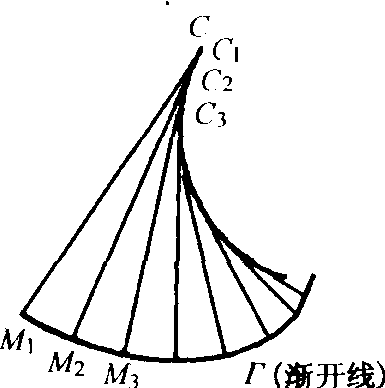 圖1
圖1 圖2
圖2漸開線方程

漸開線的性質

 圖3
圖3
漸開線的畫法
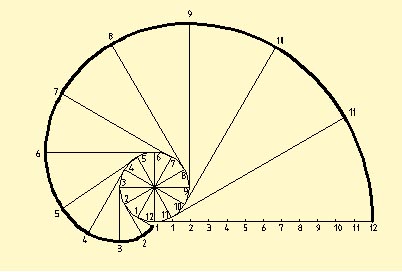 圖4漸開線畫法
圖4漸開線畫法
與一條曲線C的所有切線相交成直角的曲線Γ,稱為曲線C的漸開線(evolent)。一般的漸開線指“圓的漸開線”。在平面上,一條動直線(發生線)沿著一個固定的圓(基圓)作滾動的過程中,此直線上任意一點的軌跡,稱為此基圓的一條漸開線。
 圖1
圖1 圖2
圖2
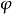

 圖3
圖3
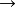
 圖4漸開線畫法
圖4漸開線畫法與一條曲線C的所有切線相交成直角的曲線Γ,稱為曲線C的漸開線(evolent)。一般的漸開線指“圓的漸開線”。在平面上,一條動直線(發生線)沿著一個固定的圓(基圓)...
基本內容 平面上一動直線沿固定圓作純滾動時﹐此直線上任意點的軌跡為該圓的漸開線(見圖 漸開線的形成 )。這一動直線BK 稱為發生線﹐固定圓O 1稱為基圓。K...
鍵齒在圓柱(或圓錐)面上且齒形為漸開線的花鍵稱為漸開線花鍵。漸開線花鍵連線採用齒形定心...
延伸漸開線編輯 鎖定 本詞條缺少信息欄、名片圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!中文名稱 延伸漸開線 英文名稱 prolate involute 定義 在...
端面齒廓為漸開線的蝸桿稱為漸開線蝸桿。就幾何性質來說,漸開線蝸桿就是漸開線斜齒輪,它相當於一個少齒數(齒數等於蝸桿頭數)、大螺旋角的漸開線圓柱斜齒輪。根據...
漸開線測量儀 involute measuring instrument:測量漸開線齒形的齒輪測量工具(見長度測量工具),常見的有單盤式和萬能式兩種。...
漸開線圓柱齒輪是齒輪中的一種。齒輪的齒形由漸開線和過渡線組成時,便被稱為漸開線齒輪。具有角速不變的優點。...
漸開線齒廓編輯 鎖定 本詞條缺少信息欄、名片圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!中文名稱 漸開線齒廓 英文名稱 involute profile 定義 齒...
《圓柱直齒漸開線花鍵(米制模數 齒側配合)(第9部分):量棒(GB/T 3478.9-2008)》主要參考了ISO 4156—2:2005《圓柱直齒漸開線花鍵(米制模數 齒側配合)第2...
《漸開線圓柱齒輪傳動》是2012年1月機械工業出版社出版的圖書,作者是張展。該書主要介紹了漸開線圓柱齒輪傳動的知識。...
縮短漸開線編輯 鎖定 本詞條缺少信息欄、名片圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!中文名稱 縮短漸開線 英文名稱 curtate involute 定義 在...
一種性能穩定可靠的標準計量器具如圖。它的漸開線齒面是檢定各種漸開線儀器的標準,用於傳遞齒輪漸開線參數量值、修正儀器示值、確定儀器示值誤差。...
球面漸開線編輯 鎖定 本詞條缺少信息欄、名片圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!是一種基於空間偏微分形式得出的空間曲線...
《漸開線齒輪行星傳動的設計與製造》是一本由顏思健著、漸開線齒輪行星傳動的設計與製造編委編的書籍。機械工業出版社於2002-01-01出版該書。《漸開線齒輪行星傳動的...
萬能漸開線檢查儀是一種測量儀器,用於測量漸開線齒輪齒形誤差。...... 萬能漸開線檢查儀是一種測量儀器,用於測量漸開線齒輪齒形誤差。目錄 1 萬能漸開線檢查儀 2 MC...
中文名稱 漸開線蝸桿基圓 英文名稱 base circle of in-volute helicoid worm 定義 漸開線蝸桿基圓柱面與端平面的交線。 套用學科 機械工程(一級學科),傳動(...
《漸開線變位齒輪傳動》是2011年國防工業出版社出版的圖書。...... 張展主編的《漸開線變位齒輪傳動》分別論述了外嚙合變位圓柱齒輪、內嚙合變位圓柱齒輪、斜齒圓柱...
▪ 電力逆變電源INV 3 漸開線函式(involute function) INV基本信息 編輯 INV指令是在將執行INV指令之前的運算結果反轉的指令,是不帶運算元的獨立指令。當X0斷...
12 GB/T5104-2008 漸開線花鍵滾刀基本型式和尺寸 2009-03-01實施13 GB/T3478.5-2008圓柱直齒漸開線花鍵(米制模數齒側配合)第5部分:檢驗 2009-05-01實施,...
漸開線上任一點法向壓力的方向線(即漸開線在該點的法線KN)和該點速度方向(垂直於OK)之間的夾角稱為該點的壓力角。顯然,圖2中的 圖2 αk即為漸開線上K點...
兩個曲線或曲面,過特定點,擁有共同的一條垂線,這條垂線就是公法線。齒輪公法線,是一條與基圓相切,與齒輪異側漸開線相交的直線。公法線,也是兩個物體接觸點各自...
機器齒輪齒兩側曲線(齒郭曲線)大多採用漸伸線,以獲得穩定轉動比,保證運轉平穩,減小震動,稱為漸開線齒輪。參考資料 1. 沈以淡.簡明數學詞典 詞條漢英對照:北京...
蝸桿是指具有一個或幾個螺旋齒,並且與蝸輪嚙合而組成交錯軸齒輪副的齒輪。其分度曲面可以是圓柱面,圓錐面或圓環面,有阿基米德蝸桿、漸開線蝸桿、法向直廓蝸桿、...
