漏斗圖是由 Light 與 Pillemer於1984年所提出，並由 Egger 等人深入探討，是Meta分析的有用工具。漏斗圖結合相關的統計檢驗，在系統評價中檢查研究是否存在報告偏倚的可能性。
漏斗圖是一個簡單的散點圖，反映研究在一定樣本量或精確性下單個研究的干預效應估計值。漏斗圖最常見的是在橫軸為各研究效應估計值，縱軸為研究樣本量。
干預措施療效的比率指標（如比值比、風險比）要在對數尺度上繪製，這能使同樣大小、但方向相反的療效值（如比值比0.5、比值比2）與1.0等距。對以連續性（數值型）尺度表示的結局（如血壓、抑鬱評分），應以均數差或標準化均數差衡量干預措施療效，這些統計指標可作為漏斗圖的橫軸。
漏斗圖最初用於教育研究和心理學領域，繪製對應於不同總樣本量的效應估計值。現常建議縱軸用干預措施療效估計值的標準誤，而非樣本總量。
基本介紹
定義,圖形分布特點,原理,造成漏斗圖不對稱的不同原因,對於漏斗圖不對稱的檢驗方法,局限性,
定義
漏斗圖是一個簡單的散點圖，反映研究在一定樣本量或精確性下單個研究的干預效應估計值。漏斗圖最常見的是在橫軸為各研究效應估計值，縱軸為研究樣本量。
干預措施療效的比率指標（如比值比、風險比）要在對數尺度上繪製，這能使同樣大小、但方向相反的療效值（如比值比0.5、比值比2）與1.0等距。對以連續性（數值型）尺度表示的結局（如血壓、抑鬱評分），應以均數差或標準化均數差衡量干預措施療效，這些統計指標可作為漏斗圖的橫軸。
漏斗圖最初用於教育研究和心理學領域，繪製對應於不同總樣本量的效應估計值。現常建議縱軸用干預措施療效估計值的標準誤，而非樣本總量。
圖形分布特點
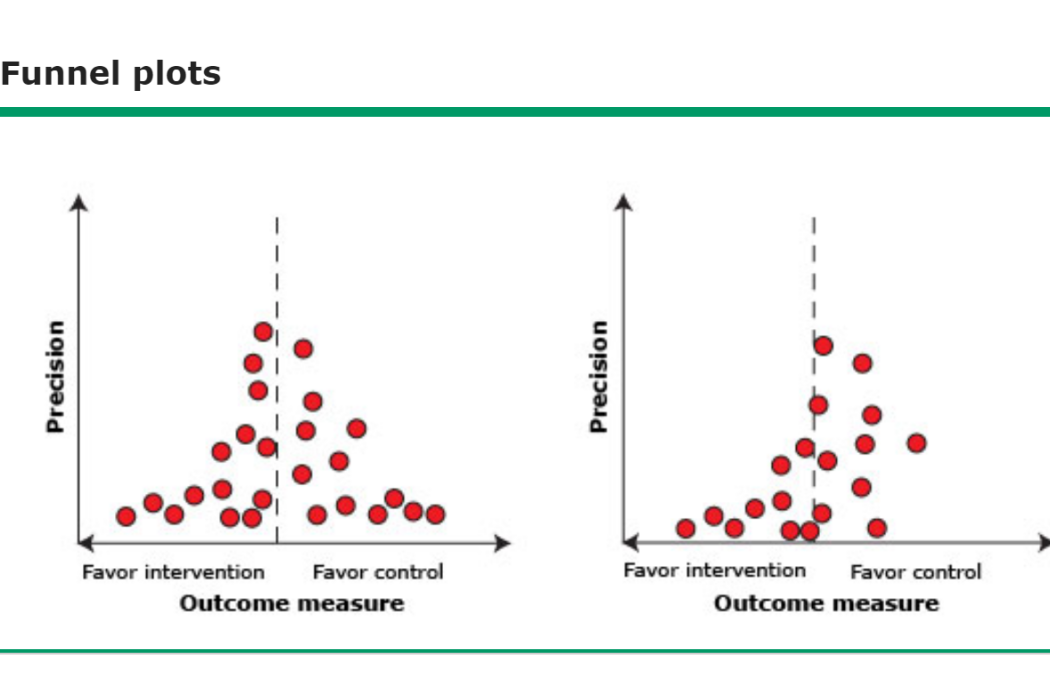
“漏斗圖”的稱法是源於隨著研究樣本量增加，干預措施療效估計值的精確度增加。因此，小樣本研究的療效估計值在漏斗圖底部更分散，而較大樣本的研究則分布得較窄。在沒有偏倚的情況下，圖像中的點應聚集成一個大致對稱的（倒置的）漏斗。圖1闡明了此種情況
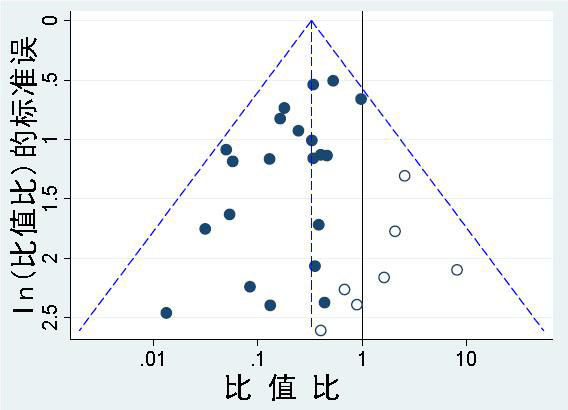
圖1 無偏倚的對稱漏斗圖
若存在偏倚，例如由於療效無統計學意義的小樣本研究尚未發表（圖A空心圈所示），將使漏斗圖外觀不對稱，圖形底角有空白（圖2）。這種情況下，Meta分析計算出的效果可能會高估干預措施療效。不對稱越明顯，越有可能存在實質的偏倚。
圖2 存在報告偏倚的不對稱漏斗圖
原理
造成漏斗圖不對稱的不同原因
儘管早就將漏斗圖不對稱與發表偏倚同等看待，但漏斗圖應視為表示小樣本研究效應（估計的干預效果在小樣本研究與大樣本研究中存在不同的一種趨勢）的通用方法，而小樣本研究效應可能取決於發表偏倚之外的其它因素。其中部分因素見表1。
表1 可能造成漏斗圖不對稱的原因——改編自Egger等
方法學質量的差異
與大樣本研究相比，小樣本研究在實施和分析的方法學上可能不嚴謹。低質量的試驗還同樣可能得出較大的干預措施療效。因此那些本來是“陰性”的試驗，如果實施和分析得當，可能變為“陽性”（圖3）。
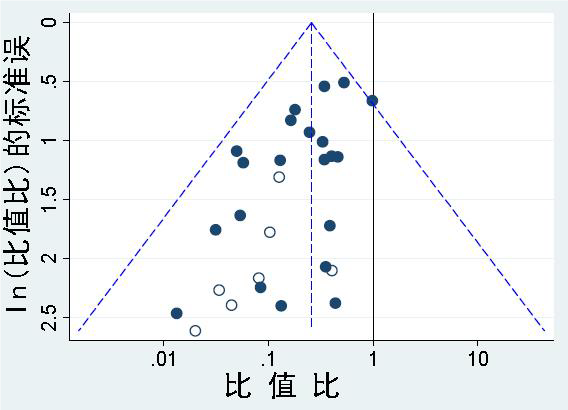
圖3 方法學質量不高、進而誇大干預措施療效估計值的小樣本研究
真實的異質性
干預措施療效真實的異質性也會使漏斗圖不對稱。比如，僅在就干預措施影響的結局而言處於高風險的患者中，才能看出干預的實質獲益；而早期階段的小樣本研究更有可能納入這些高風險患者。此外，小樣本試驗往往在大樣本試驗確立前就已經實施，在干預療程期間內標準治療可能已經得到改進（使大樣本試驗中干預措施的療效偏小）。而且，有些干預措施在大樣本試驗里可能實施得不徹底，這樣也可能會使干預措施的療效估計值偏小。最後，當然有可能僅僅是機遇的原因使漏斗圖不對成得到。Terrin等認為漏斗圖不適用於存在異質性的Meta分析，因為發起漏斗圖的前提條件是所有研究來自潛在的同一總體。
在解釋漏斗圖時，系統評價作者要能區分表1列舉的造成漏斗圖不對稱的各個可能原因。對特定干預措施及其在不同研究中實施的環境的了解，有助於找出導致漏斗圖不對稱的實際存在的異質性。
值得留意的是，目測解釋漏斗圖本身就有主觀性。所以，我們這裡將討論對漏斗圖不對稱進行統計檢驗，並探討統計檢驗多大程度上能有助於客觀解釋漏斗圖。如果系統評價作者擔心小樣本研究效應影響Meta分析結果，他們可能想進行敏感性分析，以進一步探索Meta分析對於漏斗圖不對稱原因的不同假設所得結論的穩定性。
有個可強化漏斗圖的提議，即引入等高線，這些等高線相當於所謂有統計學意義（P=0.01、0.05、0.1等等）的“里程碑”。這樣做能夠兼顧研究效應估計值的統計學顯著性，以及被視為缺失的研究。這種“經等高線強化的”漏斗圖可幫助系統評價作者鑑別因發表偏倚造成的不對稱及其它因素所致的不對稱。
對於漏斗圖不對稱的檢驗方法
漏斗圖不對稱（小樣本研究效應）的檢驗方法檢驗估計的干預療效和研究樣本量的測量值（如干預措施療效的標準誤）間的聯繫是否大於機遇產生的聯繫。採取連續性（數值型）尺度測量結局合理而直接。用Egger等推薦的方法，我們可用干預措施療效估計值的標準誤對其進行線性回歸，權重為干預措施療效估計值的方差的倒數，以尋找干預措施療效及其標準誤間的直線關係。如果無效假設是沒有小樣本研究效應，該直線將垂直於橫軸。如果幹預措施療效及標準誤間的聯繫愈大，漏斗斜線將越偏離中垂線。需要注意，權重對於確保回歸估計值不受小樣本研究的主導很重要。
如果結局指標屬於二分類，干預措施療效以比值比表示，則Egger等推薦的方法相當於對數比值比及對數比值比標準誤間的線性回歸，權重為對數比值比方差的倒數。迄今為止，本法系漏斗圖不對稱最常用的檢驗法。遺憾的是，這種方法還是存在統計學問題，因為即使沒有小樣本研究效應，對數比值比的標準誤在數學上依然和比值比的大小有關。這會使以對數比值比繪製的漏斗圖不對稱，意味著用Egger等使用的檢驗法求得的P值過小，從而得到假陽性的檢驗結果。如果幹預措施療效很大、存在明顯的研究間異質性、或各研究發生的事件數很少、或所有研究樣本量相似，則這些問題更有可能出現。
眾多作者因此提出其它檢驗漏斗圖不對稱的方法，表2總結了這些方法。正因為發表偏倚的準確成因不得而知，才要求在根據很多發表偏倚成因假設的前提下、用模擬試驗（用計算機產生的海量的數據集來評估檢驗方法）評估這些檢驗法的特點。Rücker等報導了最為全面的研究（在檢驗的場景、實施的模擬、參照的各種檢驗等方面）（Rücker2008）。這一研究及其它已發表的模擬研究提供了對於漏斗圖不對稱檢驗的如下建議。儘管模擬研究能提供了十分有用的深入見解，但它們評價的環境不可避免的不同於某個特定的Meta分析的具體環境，因此在解釋模擬研究的結果時務須慎重。
表2 推薦的用於漏斗圖不對稱的檢驗法
大部分的這類方法學工作主要集中於用比值比表示的干預措施療效。對於以危險度或標準化均數差表示的干預措施療效，預期將出現相同的問題儘管看似合理，但需要對這種情形進一步的調查。
對於模擬試驗用的參數值的代表性，以及沒有明確的合理性但經常用於模擬發表偏倚和小樣本研究效應的機制，目前仍有爭議。不同檢驗法一些可能有效的變更仍未經檢查驗證。因此在選擇漏斗圖不對稱性的檢驗方法時，不可能給出明確建議。儘管如此，對於想要檢驗漏斗圖不對稱的系統評價作者，我們仍能夠找到3種值得考慮的方法。RevMan軟體未使用這裡任何一種檢驗法，具體使用時宜諮詢專業統計人員。
局限性
有些作者認為，對漏斗圖的目測解釋過於主觀而用處不大。尤其是，Terrin等發現，研究人員只有非常有限的能力，可以正確無誤找出受發表偏倚影響的Meta分析的漏斗圖。
漏斗圖還有個重要問題，就是有些療效估計值（如比值比、標準均數差）本來就與其標準誤相關，在漏斗圖中可引起虛假的不對稱。
此外，假如高精準度的研究與低精準度的研究在效應大小方面不同（例如因為研究不同族群所致），漏斗圖可能得出出版偏差的錯誤結論。漏斗圖的縱軸刻度大小也可能大大改變漏斗圖的外觀－－不管其是反比平方誤差或是研究大小所致。
