基本介紹
- 中文名：滑輪組
- 外文名：tackle block
- 組成：動滑輪、定滑輪
- 作用：可以省力也可以改變施力方向
- 效率決定因素：拉物體重力、動滑輪重力及摩擦
- 適用範圍：物理 生活
滑輪,定義,滑輪的歷史,省力計算,分類,定滑輪,動滑輪,滑輪組,滑輪組原理,滑輪組的分類,滑輪組的用途,滑輪組的特點,滑輪組繞法,口訣,機械效率,特點,
滑輪
定義
滑輪是槓桿的變形，屬於槓桿類簡單機械。
滑輪的歷史
關於滑輪的繪品最早出現於一幅西元前八世紀的亞述浮雕。這浮雕展示的是一種非常簡單的滑輪，只能改變施力方向，主要目的是為了方便施力，並不會給出任何機械利益。在中國，滑輪裝置的繪製最早出現於漢代的畫像磚、陶井模。
古希臘人將滑輪歸類為簡單機械。早在西元前400年，古希臘人就已經知道如何使用複式滑輪了。大約在西元前330年，亞里斯多德在著作《機械問題》（《Mechanical Problems》）里的第十八個問題，專門研討“複式滑輪”系統阿基米德貢獻出很多關於簡單機械的知識，詳細地解釋滑輪的運動學理論。據說阿基米德曾經獨自使用複式滑輪拉動一艘裝滿了貨物與乘客的大海船，西元一世紀，亞歷山卓的希羅分析並且寫出關於複式滑輪的理論，證明了負載與施力的比例等於承擔負載的繩索段的數目，即“滑輪原理”。
1608年，在著作《數學紀要》（《Mathematical Collection》）里，荷蘭物理學者西蒙·斯特芬表明，滑輪系統的施力與負載之間移動路徑的長度比率，等於施力與負載之間的反比率。這是雛型的虛功原理。
在我國，約完成於周安王14年癸巳（公元前388年）墨翟（人稱墨子）和他的弟子們寫的著作《墨經》中就有關於滑輪的記載。中心軸固定不動的滑輪叫定滑輪，是變形的等臂槓桿，不省力但可以改變力的方向。中心軸跟重物一起移動的滑輪叫動滑輪，是變形的不等臂槓桿，能省一半力，但不改變力的方向。實際中常把一定數量的動滑輪和定滑輪組合成各種形式的滑輪組。滑輪組既省力又能改變力的方向。
省力計算
公式：s=nh。 v繩=n*v物 F拉=（1/n）*G總
s：繩子自由端移動的距離。 v繩：繩子自由端移動（上升/下降）的速度
h：重物被提升的高度。 v物：物體移動（上升/下降）的速度
n：承重的繩子段數（與動滑輪相連的繩子）。 G總：物重+滑輪重（G物+G滑）。
其次，按要求確定定滑輪個數，原則是：一般的：兩股繩子配一個動滑輪。
分類
滑輪有兩種：定滑輪和動滑輪 ，組合成為滑輪組，它既可以省力又可以改變力的方向。
定滑輪
定義：固定在一個位置轉動而不移動的的滑輪叫定滑輪。
定滑輪的作用是改變力的方向
動滑輪
動滑輪實質是動力臂為阻力臂二倍的槓桿，省1/2力多費1倍距離.
( 註：上句前提為拉力方向為豎直方向方可省1/2的力，若呈斜拉狀態，則拉力多於省的1/2的力，且角度越大越費力。）
滑輪組
滑輪組：由定滑輪跟動滑輪組成的滑輪組，既省力又可改變力的方向.
滑輪組用幾段繩子吊著物體，提起物體所用的力就是總重的幾分之一.繩子的自由端繞過動滑輪的算一段，而繞過定滑輪的就不算了.
使用滑輪組雖然省了力，但費了距離，動力移動的距離大於重物移動的距離.
滑輪組原理
有的中學物理教科書認為，利用滑輪組運輸或提升貨物，只能省力，但不能省功，中學物理教科書的上述結論對從事機械傳動設計工作的工程師影響極大，由於汽車、火車、輪船等運輸裝置和各種機械裝置在使用的過程中會頻繁地出現啟動、加速、減速、停止等各種運動，並在啟動、加速、減速、停止等各種運動過程中消耗大量的能量，完全需要在理論上說明怎樣設計或使用汽車、火車、輪船等運輸裝置的傳動系統，以使其處於最佳節能狀態，但中學物理教科書的上述結論使得機械工程師在從事機械傳動設計時，以及在指導人們使用運輸車輛和機械裝置時，往往忽略了滑輪組的段數或減速機的傳動比在各種狀態下與節能的關係，造成現有的許多運輸車輛和機械傳動裝置在運行過程中的能量消耗較高，輸送貨物數量較少。
下面通過分析兩個物理習題的方式說明利用滑輪組牽引物體，不僅可以省力，而且可以通過將更多的物體輸送至目的地的形式節約能源。
對於沿水平方向作牽引物體運動的滑輪組
分析如下：
一個質量為m的物體M放置在水平面上，利用滑輪組通過繩子與物體M相連，繩子牽引物體M的段數為K，繩子的牽引力為F，利用動力裝置使物體M沿水平面由靜止狀態開始作加速運動，則由牛頓運動定律可知：
KF=ma2 （1）
式中a2為物體M的加速度，並且
a2=a1/K （2）
式中a1為滑輪組輸入端繩子的加速度，解（1）、（2）式可得：
a1=K2F/m （3）
使用滑輪組的目的是運輸或提升一定數量貨物到達目的地，每個從事具體勞動的人都希望多拉快跑，即省力、又迅速地完成工作。為了對比使用滑輪組與不使用滑輪組的區別，令滑輪組輸入端繩子的加速度在使用滑輪組與不使用滑輪組時都為a1值，在此狀態下動力裝置輸出的功率相等，設不使用滑輪組時（K=1）動力裝置運輸的物體M質量為m′，使用滑輪組時動力裝置運輸的物體M質量為m，則有：
F/m′=K2F/m （4）
化簡後可得：
m=K2m′ （5）
但使用滑輪組時動力裝置運輸物體M的距離是不使用滑輪組時的L/K，為了便於對比，分別令兩種狀態下的動力裝置工作K次，這樣一來，使用滑輪組的動力裝置就可將質量為K2m′的貨物輸送至L距離，不使用滑輪組的動力裝置則將質量為Km′的貨物都輸送L距離，此時通過對比可見，使用滑輪組時動力裝置運輸的物體M質量m為不使用滑輪組時動力裝置運輸的物體M質量m′的K倍。
當物體M的運動存在摩擦阻力f時，則式（1）變為
KF-f=ma2 （6）
其中f=μmg，μ為摩擦係數。
解（2）、（6）式，並將f=μmg帶入可得：
a1=（K2F-Kμmg）/m （7）
同樣令滑輪組輸入端繩子的加速度在使用滑輪組與不使用滑輪組時都為a1值，在此狀態下動力裝置消耗的功率相等，設不使用滑輪組時（K=1）動力裝置運輸的物體M質量為m′，使用滑輪組時動力裝置運輸的物體M質量為m，則有：
（F-μm′g）/m′=（K2F-Kμmg）/m （8）
化簡後可得：
m=K2Fm′/（F+Kμm′g -μm′g） （9）
同樣地，使用滑輪組時動力裝置運輸物體M的距離是不使用滑輪組時的L/K，為了便於對比，分別令兩種狀態下的動力裝置工作K次，這樣一來，使用滑輪組的動力裝置就可將質量為K2Fm′/（F+Kμm′g -μm′g）的貨物輸送至L距離，使用滑輪組時動力裝置運輸的物體M質量m為不使用滑輪組時動力裝置提升的物體M質量m′的KF/（F+Kμm′g-μm′g）倍。也就是說，利用滑輪組牽引物體，在某些條件下使運輸車輛和機械傳動裝置不僅可以省力，而且可以通過將更多的物體輸送至目的地的形式節約能源。
由於汽車、火車、輪船等運輸裝置在使用的過程中會頻繁地出現啟動、加速、減速、停止等各種運動，並在啟動、加速、減速、停止等各種運動過程中消耗大量的能量，上述結論可以在理論上被用來指導和說明設計或使用汽車、火車、輪船等運輸裝置的傳動系統，以使其處於最佳節能狀態。例如，汽車、火車、輪船等運輸裝置在啟動、加速階段可以採用大傳動比的傳動系統，開足馬力全力衝刺，而不要採用傳動比小的傳動系統。
對於沿垂直方向作牽引物體運動的滑輪組或者是減速機分析如下：
一個質量為m的物體M懸掛在空中，利用滑輪組的輸出端通過繩子與物體M相連，繩子牽引物體M的段數為K，繩子的牽引力為F，利用動力裝置使物體M在空中由靜止狀態開始作向上的加速運動，則由牛頓運動定律可知：
KF-mg=ma2 （10）
式中a2為物體M的加速度，並且
a2=a1/K （11）
式中a1為滑輪組輸入端繩子的加速度，解（11）、（12）式可得：
a1=（K2F-Kmg）/m （12）
在此狀態下動力裝置輸出的功率相等，設不使用滑輪組時動力裝置運輸的物體M質量為m′，使用滑輪組時動力裝置運輸的物體M質量為m，則有：
（F-m′g）/m′=（K2F-Kmg）/m （13）
化簡後可得：
m=K2m′/〔1+（K-1）m′g/F〕 （14）
但使用滑輪組時動力裝置提升物體M的高度是不使用滑輪組時的h/K，為了便於對比，分別令兩種狀態下的動力裝置工作K次，這樣一來，使用滑輪組的動力裝置就可將質量為K2m′/〔1+（K-1）m′g/F〕的貨物提升至h高度，不使用滑輪組的動力裝置則將質量為Km′的貨物都提升至h高度，此時通過對比可見，使用滑輪組時動力裝置提升的物體M質量m為不使用滑輪組時動力裝置提升的物體M質量m′的K/〔1+（K-1）m′g/F〕倍。
當物體M的運動存在摩擦阻力f時，則式（11）變為
KF-mg-f=ma2 （15）
其中f=μmg，μ為摩擦係數。
解（12）、（16）式，並將f=μmg帶入可得：
a1=（K2F-Kmg-Kμmg）/m （16）
同樣令滑輪組輸入端繩子的加速度在使用滑輪組與不使用滑輪組時都為a1值，在此狀態下動力裝置輸出的功率相等，設不使用滑輪組時動力裝置提升的物體M質量為m′，使用滑輪組時動力裝置提升的物體M質量為m，則有：
（F-m′g-μm′g）/m′=（K2F-Kmg-Kμmg）/m （17）
化簡後可得：
m=K2Fm′/（F+Km′g+Kμm′g-m′g-μm′g） （18）
同樣地，使用滑輪組時動力裝置提升物體M的高度是不使用滑輪組時的h/K，為了便於對比，分別令兩種狀態下的動力裝置工作K次，這樣一來，使用滑輪組的動力裝置就可將質量為K2Fm′/（F+Km′g+Kμm′g-m′g-μm′g）的貨物提升至h距離，不使用滑輪組的動力裝置則將質量為Km′的貨物都提升h高度，此時通過對比可見，使用滑輪組時動力裝置提升的物體M質量m為不使用滑輪組時動力裝置提升的物體M質量m′的KF/（F+Km′g+Kμm′g-m′g-μm′g）倍。也就是說，利用滑輪組或減速機提升物體，在某些條件下使運輸車輛和機械傳動裝置不僅可以省力，而且可以通過將更多的物體提升至目的地的形式節約能源。
由於上分析可知，對於電梯、吊車等各種縱向運輸裝置，在啟動、加速階段可以採用大傳動比的傳動系統，而不要採用傳動比小的傳動系統。
通過以上分析可知，令動力裝置通過滑輪組或減速機對物體進行輸送，無論是沿水平方向，還是沿垂直方向，都能夠在消耗一定能量的條件下，將更多的貨物輸送到目的地。
滑輪組的組裝:滑輪組
滑輪組是由若干個定滑輪和動滑輪匹配而成，可以達到既省力又改變力作用方向的目的。使用中，省力多少和繩子的繞法，決定於滑輪組的使用效果。動滑輪被幾根繩子承擔，力就是物體和動滑輪總重的幾分之一。原則是：n為奇數時，繩子從動滑輪為起始。用一個動滑輪時有三段繩子承擔，其後每增加一個動滑輪增加二段繩子。如：n=5，則需兩個動滑輪（3+2）。n為偶數時，繩子從定滑輪為起始，這時所有動滑輪都只用兩段繩子承擔。如：n=4，則需兩個動滑輪（2+2）。
其次，按要求確定定滑輪個數，原則是：一個動滑輪一般配一個定滑輪。力作用方向不要求改變時，偶數段繩子可減少一個定滑輪；要改變力作用方向，需增加一個定滑輪。
綜上所說，滑輪組設計原則可歸納為：奇動偶定；一動配一定，偶數減一定，變向加一定。
對於繞繩方法,有一點切記:繩不可相交.其實繞繩難的就數滑輪組拉,只要掌握了要決,那就一點不難拉.滑輪組在繞線時如果動滑輪少那么要先從定滑輪繞起;反之要定滑 輪少,那么要先從動滑輪繞起;如果一樣多的話還是要先繞動滑輪。
滑輪組的分類
滑輪組是由一定數量的定滑輪和動滑輪以及繞過它們的繩索組成。滑輪組具有省力和改變力的方向的功能，是起重機械的重要組成部分。滑輪組共同負擔構建重量的繩索根數稱為工作線數。通常，滑輪組的名稱以組成滑輪組定滑輪與動滑輪的數目來表示。如由四個定滑輪和四個動滑輪組成的滑輪組稱為四四滑輪組。
滑輪組的用途
為了既節省力又能改變動力的方向，可以把定滑輪和動滑輪組合成滑輪組。
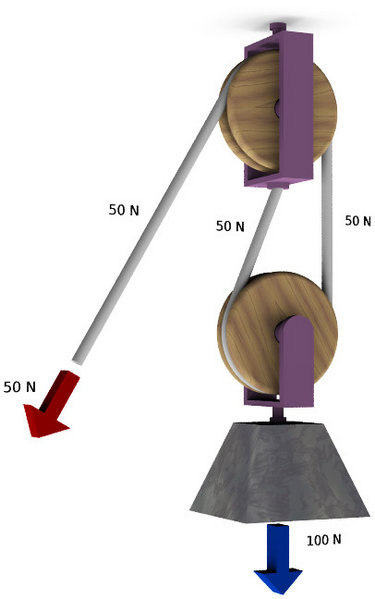
省力的大小 沒有既省力又省距離的滑輪
使用滑輪組時，滑輪組用幾段繩吊著物體，提起物體所用的力就是物重的幾分之一。
滑輪組的特點
用滑輪組做實驗，很容易看出，使用滑輪組雖然省了力，但是費了距離——動力移動的距離大於貨物升高的距離。
滑輪組繞法
畫滑輪組的繞法， 首先要分析題目要求，是要減輕幾倍力（是原來的幾分之一） F=G/n,n為承擔重物的繩子的段數。註：如果n是偶數，那么繞線的起始點在上面的定滑輪上；如果n是奇數，那么繞線的起始點在下面的動滑輪上。 即“奇動偶定”定理。
口訣
起點要在掛鈎上，反繞滑輪鄰先上。
左右過人必準確，首末定向是同方。
零定一動數段快，奇動偶定繞線忙。
不計輪重和摩擦，省力費距n當王。
機械效率
W總=W有+W額
W總=動力對機械做的功
W有=機械對物體做的功
W額=克服機械自身重力、摩擦力做的功
η=W有/W總（任何機械都不可避免的做額外功，有用功總是小於總功，所以機械效率總是小於1。機械效率通常用百分數表示）
一架絞車通過滑輪組提升重800N的物體，在1min內將物體提升3m，已知軸的半徑是4.8cm，搖柄的長是48cm，搖動搖柄時用的力是49N，計算
1.這個裝置的機械效率
2.搖絞車的人的功率 先假設絞車的效率為100%，則絞車的拉力為49/4.8*48=490（N）。
根據此力大於重物重量的一半，則：
可以假設使用一個動滑輪的滑輪組組，則：需要絞車拉繩的長度為3m*2=6m；絞車需要轉過的圈數為600（cm）/2/3.1416/4.8=19.894(圈）；人做功的距離為19.894（圈）*2*3.1416*48=6000cm。
則：
1.這個裝置的機械效率為800*300/(6000*49)*100%=81.6%
2.搖絞車的人的平均功率為49（N)*60（m）/60（s)= 49（W）。
假如假設使用兩個動滑輪的動滑輪組，則可以得出另一組結果：
1.這個裝置的機械效率為800*300/(12000*49)*100%=40.8163%
2.搖絞車的人的平均功率為49（N)*120（m）/60（s)=98（W）。
