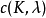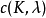準可分解可分組設計(almost resolvable groupdivisible design)是一類特殊的可分組設計，設(X，G，A)是具有型mn的可分組設計GDD[{k}，1，{m};mn]，對任一個組G∈G，若A中某些區組的族P劃分集X\G，則稱P是一個帶洞G的準平行類，若A可劃分成一些準平行類，則稱該可分組設計是準可分解的可分組設計，記為k支架。
基本介紹
- 中文名：準可分解可分組設計
- 外文名：almost resolvable groupdivisible design
- 所屬學科：數學
- 所屬問題：組合學（組合設計）
- 簡介：一類特殊的可分組設計
基本介紹,相關概念,可分組設計,成對平衡設計,
基本介紹
設(X，G，A)是具有型m的可分組設計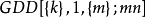
，對任一個組
，若A中某些區組的族P劃分集X\G，則稱P是一個帶洞G的準平行類，若A可劃分成一些準平行類，則稱該可分組設計是準可分解的可分組設計，記為k支架，k支架的概念是在研究可分解平衡不完全區組設計的存在性問題中形成的，對其他類型的可分解設計也有用，關於k支架的存在性，史汀生(D.R.Stinson)於1987年證明：型為m的3支架存在的充分必要條件為
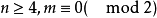且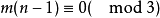
。
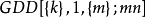
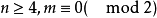
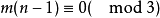
相關概念
可分組設計
可分組設計是成對平衡設計的一種推廣，常用於PBD的遞推構造，設X為v元集，G是X的某些子集，它們劃分X且稱為組，A是X的某些子集(稱為區組)的族.若X中屬於同一個組的任意兩個元不同時含於任何區組，而屬於不同組的任意兩個元恰同時含於λ個區組，則稱(X，G，A)為一個可分組設計，若組的大小均在集M中，而區組大小均在集K中，則記該可分組設計為
，若G中有ti個大小mi的組，
，則稱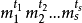
為組的型，一個型為1v的
就是一個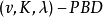
，關於可分組設計存在性的系統結果僅限於K={k}且型為mu的情形，可分組設計
存在的必要條件是：
。當k=3，4時，除兩個例外情形外，以上必要條件也是充分條件，這兩個情形是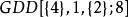
及
，它們都不可能存在。
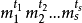
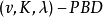
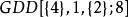
成對平衡設計
成對平衡設計是平衡不完全區組設計的一種推廣，設X為v元集，B是X的某些子集(稱為區組)的族，B中區組的大小(數)均在某個正整數集合K中，若X的任意兩個元素恰含於B的λ個區組中，則將二元組(X，B)稱為成對平衡設計，記為(v，K，λ)-PBD，當區組大小都相同時，這種特殊的成對平衡設計就是平衡不完全區組設計。
成對平衡設計的概念和方法曾對正交拉丁方及平衡不完全區組設計的存在性和構造方法的研究起過重要的作用.例如，玻色(R.C.Bose)等關於歐拉猜想的反證，哈拿匿(H.Hanani)關於區組大小為3，4，5的平衡不完全區組設計存在的充分必要條件，以及哈拿匿等關於區組大小為3，4的可分解平衡不完全區組設計存在的充分必要條件等.在這些重要的工作中，成對平衡設計作為研究組合設計的一般工具也得到了發展.威爾森(R.M.Wilson)於20世紀70年代引入了PBD閉集的概念，在此基礎上形成的PBD閉集方法不僅簡化了一些經典結果的證明，也為統一處理新提出的各種組合設計的存在性問題提供了有效的途徑，若
