基本介紹
- 中文名:湍流運動
- 外文名:turbulent motion
- 產生原因:流體系統的不穩定性
- 特徵:流體微團運動的隨機性
- 判斷依據:雷諾數Re
定義
層流與湍流
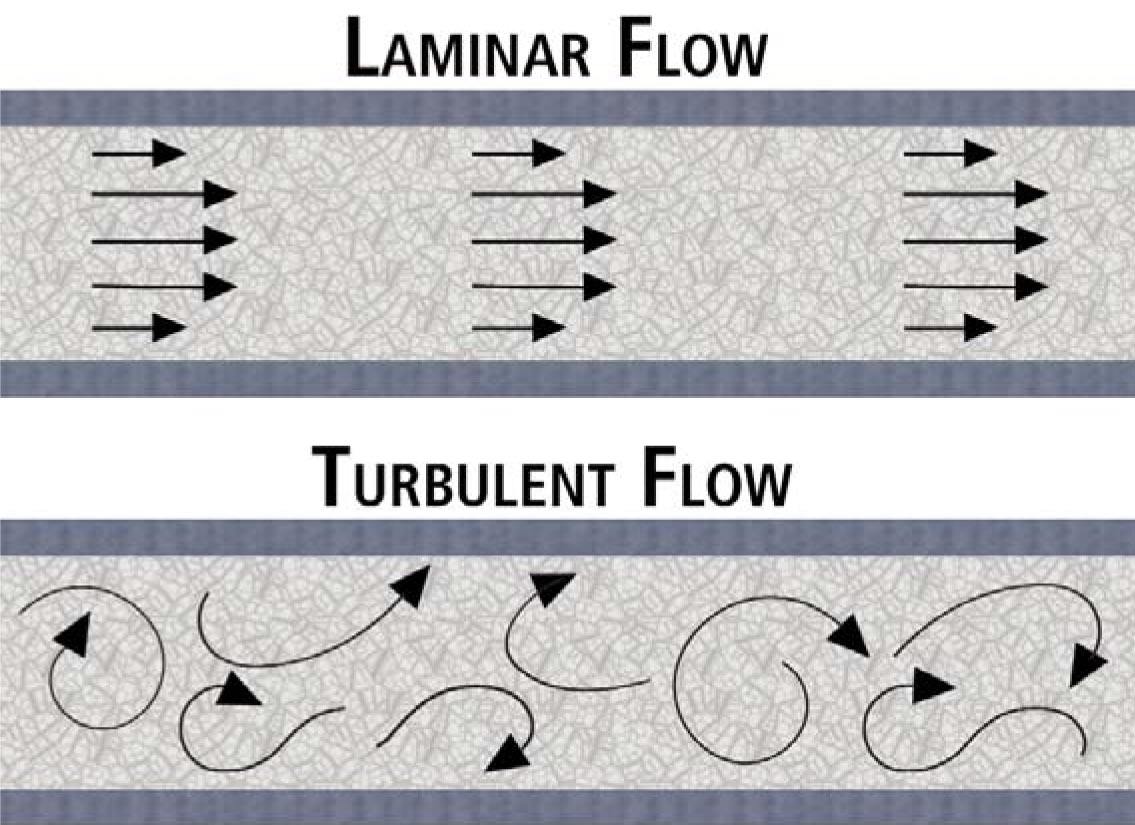 層流與湍流
層流與湍流雷諾數
 雷諾數的計算
雷諾數的計算
湍流產生的原因
湍流的特徵
 湍流的特徵
湍流的特徵湍流的利弊
 湍流的實例
湍流的實例湍流理論
湍流的半經驗理論和模式理論
數值模擬預測湍流流動的方法
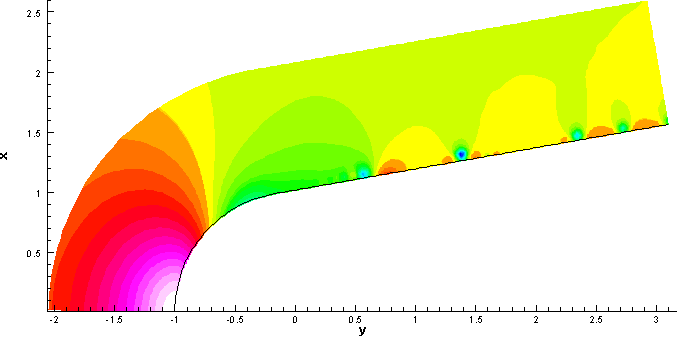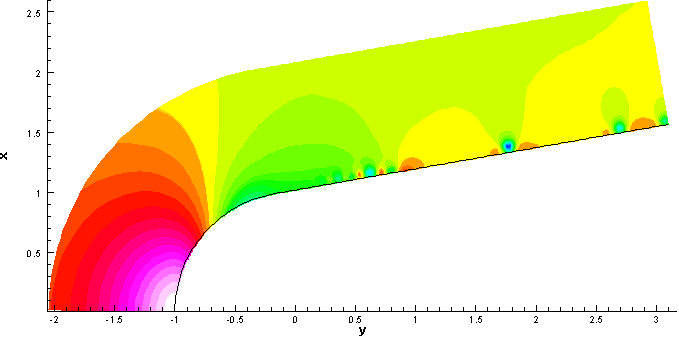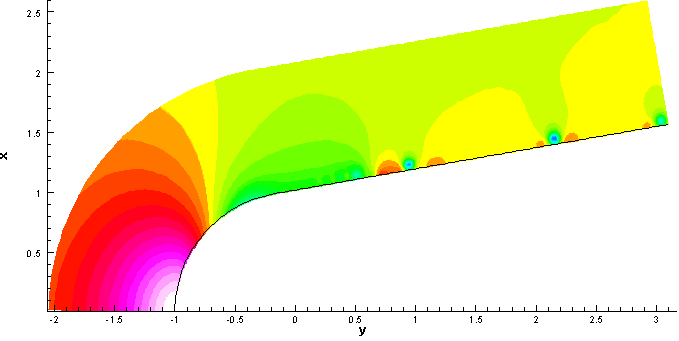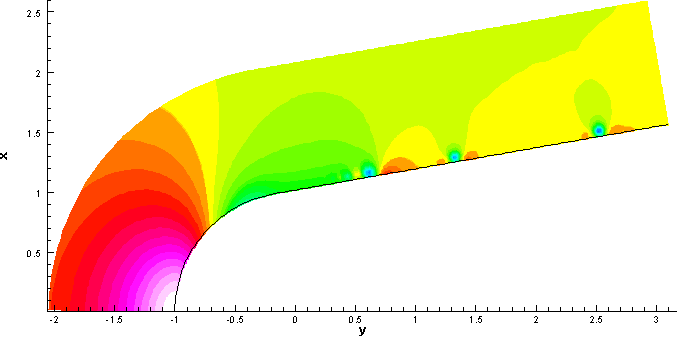 湍流直接數值模擬
湍流直接數值模擬
 層流與湍流
層流與湍流 雷諾數的計算
雷諾數的計算
 湍流的特徵
湍流的特徵 湍流的實例
湍流的實例 湍流直接數值模擬
湍流直接數值模擬湍流是流體的一種流動狀態。當流速增加到很大時,流線不再清楚可辨,流場中有許多小漩渦,層流被破壞,相鄰流層間不但有滑動,還有混合,形成湍流,又稱為亂流、擾流...
湍流是一種高度複雜的三維非穩態、帶旋轉的不規則流動。在湍流中的流體的各種物理參數,如速度、壓力、溫度等都隨時間與空間發生隨機的變化。...
湍流強度是描述風速隨時間和空間變化的程度,反映脈動風速的相對強度,是描述大氣湍流運動特性的最重要的特徵量。湍流產生的原因主要有兩個,一個是當氣流流動時,氣流...
大氣湍流是大氣中的一種重要運動形式,它的存在使大氣中的動量、熱量、水氣和污染物的垂直和水平交換作用明顯增強,遠大於分子運動的交換強度。大氣湍流的存在同時對...
湍流理論是一個有關湍流成因的理論學說,研究湍流的起因和特性的理論,包括兩類基本問題:①湍流的起因,即平滑的層流如何過渡到湍流;②充分發展的湍流的特性。...
大氣層中空氣密度的無規則起伏稱為大氣湍流。湍流對光束傳輸的影響稱為湍流效應。在地球表面,熱空氣上升,冷空氣下沉,形成空氣對流。這樣,在大氣中各點的溫度和密度...
層流和湍流是流體流動的一種性質。流體流動時,如果流體質點的軌跡(一般說隨初始空間坐標x、y、z和時間t而變)是有規則的光滑曲線(最簡單的情形是直線),這種流動...
常用的湍流模型可根據所採用的微分方程數進行分類為:零方程模型、一方程模型、兩方程模型、四方程模型、七方程模型等。...
湍流應力,又稱雷諾應力,是指雷諾方程中脈動動量交換所引起的附加應力。它包括附加法向應力和附加剪應力。...
流體是液體和氣體的總稱,由大量的、不斷地作熱運動而且無固定平衡位置的分子構成的,它的基本特徵是沒有一定的形狀和具有流動性。流體都有一定的可壓縮性,液體可...
《工程湍流》是2011年科學出版社出版的圖書,作者是劉士和。...... 第2章 工程湍流運動的基本方程2.1 單相湍流運動的基本方程2.2 散粒體運動的基本方程...
湍流是流體的一種流動狀態。當流速很小時,流體分層流動,互不混合,稱為層流,也稱為穩流或片流;逐漸增加流速,流體的流線開始出現波浪狀的擺動,擺動的頻率及振幅隨...
內燃機缸內的氣流運動,除了渦流、滾流和擠流外,還存在著一種隨機、非定常、有旋的流動,即湍流或紊流。湍流是自然界普遍存在的流體運動,它只有在流體高速流動(高...
湍流剪應力又可稱為湍流切應力。流體作湍流運動時所產生的應力,除了粘性應力外尚有附加的應力,包括法向附加應力和切向附加應力,這些附加的應力都是湍流所特有的。...
湍流數值計算(numerical computation of turbulent flow),是指用合適的湍流模式和數值方法並運用高速電子計算機算出湍流參量的方法。它主要有兩種:平均方法和數值實驗。...
在植物群落附近由於風速梯度而形成各種大小的渦旋氣團,氣團的不規則運動就形成湍流,在湍流運動過程中,對熱量、水和二氧化碳等物質進行輸送。在近地層,湍流引起的空氣...
湍流層是離地面高度90-110km之間處於熱層底部,風向風速在時間上空間上變動很大,湍流活躍的氣層。...
中文名 海水湍流混合 通過海水流體塊的湍流運動,進行彼此間熱量、鹽量和動量的交換過程。這種混合效應十分顯著。主要靠外力(風,潮流等)的攪動引起。在垂直方向和...
《大氣湍流基礎》是2014年北京大學出版社出版的圖書,作者是張宏昇。...... 全書分為八章,內容包括:大氣湍流概論、大氣湍流基本控制方程、大氣湍流運動、湍流統計描述...
湍流渦全稱湍流渦旋,簡稱渦旋。湍流運動中具有有組織流動結構和物理特性的部分。形象上如水流中的渦旋,但對於某一特定的湍渦,其出現和維持在時間上和空間上都是...
湍流是自然界和工程中普遍存在的一種十分複雜的流動現象。流體在近壁面的湍流成為壁湍流。...
高空中也有風帶,有的風帶中,風向風速都在急速變化,空氣還伴隨上下運動,飛機經過會產生強烈的擺動、顛簸,叫高空遄流。湍流,肉眼看不到,雷達也探測不到,只有飛機...
湍流度,又稱湍流強度,是度量氣流速度脈動程度的一種標準,通常用脈動速度均方和與時均速度之比來表示脈動的大小。湍流顯然是一個複雜的隨機過程,並且不用簡單明確...
湍流是流體的一種流動狀態。空氣湍流與管道的形狀、大小以及管道的材料有關。在化工原理中常用雷諾準數來判斷流體的流動狀況。 對於一般的管道,當雷諾數Re<2300時,...
湍流半經驗理論是指研究湍流通量輸送與有關屬性空間導數關係的理論。由於湍流擴散+分複雜,現有理論多為經驗和半經驗理論,包括梯度-輸送理論、普朗特混合長理論、卡門...
各向同性湍流,是一種最簡單的理想化湍流,其中時間平均湍流量(u一樣有效值)具有在每個位置相同的值。另一方面均相流是其中的湍流量在任何給定位置都在所有方向是...
