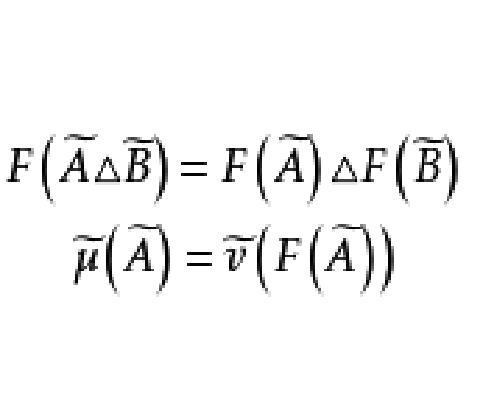測度代數

測度代數(measure algebra)定義了正測度的σ代數，若F既是代數又是測度環，則稱F是一個測度代數。若測度μ是有限的或σ有限的，則稱相應的測度代數(測度環)為有限的或σ有限的測度代數(測度環)。

基本介紹

• 中文名：測度代數
• 外文名：measure algebra
• 所屬學科：數學
• 相關概念：機率空間、保測變換等

基本介紹

定義

設 為機率空間，在上引入等價關係： ，令 ={ | 為 的等價類， }，將中的並、交、差、補、對稱差、包含關係自然延拓到 上，並定義 ，此時稱 為 的測度代數。

測度代數的同構

若存在一一在上的映射 ，使

則稱兩個測度代數 是同構的，對保測系統 ，令

設 分別為 上的保測變換，若存在同構 ，使，則稱T和S是共軛的。容易證明，同構⇒共軛⇒譜同構，但反之未必成立。在一定條件下，例如，當X，Y為完備可分度量空間，為波萊爾機率空間時，同構與共軛是等價的。

其他介紹

定義 設為機率空間，在上定義等價關係：稱A和B為等價的()若且唯若。令為其等價類空間，那么在由的交、並、補運算誘導過來的運算元下，成為代數。由測度m誘導的上的測度為(其中為所在的等價類)。偶對稱為測度代數。

依據上面的觀點，稱與為“等價的”是指它們誘導的測度代數為同構的。

定義 設與為測度空間，而為相應的測度代數，兩個測度代數為同構的是指存在雙射，它保持補、可數並和可數交運算且滿足，兩個機率空間稱為共軛的是指它們的測度代數為同構的。

一般地說，共軛要比同構弱，但在某些條件下二者是等價的。

定理 設為完備可分的度量空間，設為它們的代數而分別為上的機率測度，令為它們測度代數間的同構，那么存在,滿足，同時存在一個可逆保測映射，使得,，如果為另一個從到誘導的同構，則

相應的結論對於保測同態也是成立的(它們由保測變換誘導(不必為可逆的))。