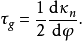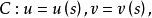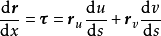測地撓率

曲面在其上點P處沿給定方向的測地撓率(geodesic torsion)是通過點P的沿給定方向的測地線的撓率。曲面上的一條曲線在點P處的測地撓率是曲面在點P處沿該曲線方向的測地撓率。

基本介紹

• 中文名：測地撓率
• 外文名：geodesic torsion
• 所屬學科：數學
• 相關概念：測地線、撓率、法曲率等

定義

在曲面上，過P點的非直測地線以單位切向量

為初始方向，我們稱此測地線C在P點的撓率為曲面在P點沿方向的測地撓率，記作。

或者說：在曲面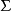上點P處給定一個單位向量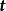，作過點P以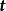為切向量的測地線C，則C在點P處的撓率，稱為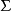在點P處沿方向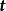的測地撓率，記作。

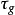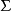
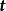
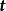
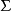
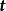
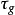
另一種記法：曲面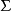上點P的方向的測地撓率為

曲面在點P的方向的測地撓率為上通過點P以為切方向的測地線在這點的撓率。

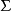
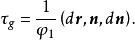
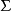
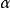
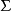
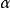
計算公式

定理1 在曲面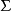上過P點非直測地線C(設C的方程為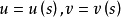：)，在該點沿方向的測地撓率為

測地撓率的另一種形式的計算公式是

其中，為曲面的第一基本齊式。

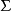
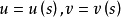
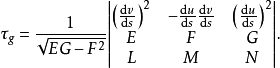
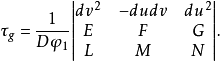
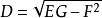
曲面上異於直線的漸近曲線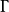的每點的撓率等於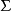在這點沿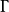方向的測地撓率。

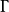
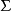
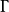
曲線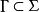是曲率線↔沿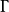的測地撓率。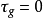

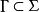
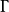
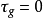
推論2 曲面上一條曲線C 為曲率線的充分必要條件是在曲線C上每點處，關於它的切方向上的測地撓率為零。

定理3 測地撓率的貝特朗公式

其中為主曲率，是曲面在點P的方向與第一主方向的夾角。

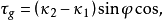
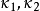
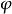
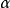
定理4測地撓率與法曲率之間有關係