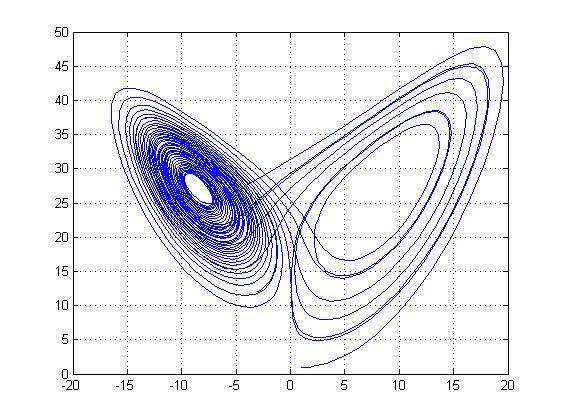
基本介紹
- 中文名:混沌振動
- 性質:一種機械振動理論
- 領域:振動力學
發展現狀,混沌振動的識別,產生機理,混沌振動在工程中的利用,
發展現狀
混沌振動是一種由確定性系統產生對於初始條件極為敏感而具有內稟隨機性和長期預測不可能性的往復非周期運動。關於混沌振動的研究已成為振動力學中一個蓬勃發展的新領域。它不僅對數學、物理、力學的各個分支有重大促進,而且也為化學、生物學、生態學、經濟學等學科提供一種分析問題的新思路,甚至對人類認識自然界的一些基本概念如因果性、決定論、隨機性等也有深刻啟示。
混沌振動作為機械振動理論的新分支,正在成為一個日趨活躍的研究領域。對於確定性機械系統,產生混沌振動的先決條件是系統的非線性,如分段的或不連續變化的系統剛度、阻尼和表面摩擦。此外,由於局部衝擊而造成的局部變形和彈性波也能導致系統的非線性。對於混沌振動,主要研究機械系統中的混沌行為。這種研究在過去的20多年裡發展非常迅速,已取得了豐碩的成果。
混沌振動的識別
混沌識別是混沌振動研究的前提和首要條件。有了識別混沌的標準或依據,才有可能研究與混沌有關的其他問題。21世紀初,混沌動力學系統的一些基本特性,如對初始條件的敏感性、奇怪吸引子及其分維特性等,已為人們所普遍接受,而且已找到判別的定量方法(Lyapunov指數)和定性方法(如功率譜的寬頻性,相軌圖的複雜性等),用以對混沌振動的存在性進行識別和證實。
其一般步驟為:(1)將實際的動力學系統抽象為理論模型;(2)根據有關學科的理論,建立系統的動力學方程;(3)有時結合非線性科學的有關理論,如諧波平衡法、平均法、Floquet理論等,對方程進行必要的變換處理;(4)鑒於方程的非線性和複雜性,往往採用數值積分對方程進行求解;(5)藉助分叉圖、Poincare圖、功率譜(FFT)、相軌圖和LyaPunov指數等,從理論上對系統混沌振動的存在性加以識別或證實。
綜合有關文獻,產生混沌振動的機械系統主要有如下幾類:(1)有間隙或摩擦的轉子系統;(2)有阻尼或庫倫摩擦的非線性振動系統比;(3)非線性彈性聯軸節系統;(4)磁懸浮振動系統。此外,還有變截面彎梁、工具機顫振和路面車輛系統等。
產生機理
混沌研究表明,如果一個動力學系統具有Smale馬蹄變換,則意味著有混沌存在。在實際問題中,更加切實可行的辦法是判斷Melnikov函式是否具有簡單零點。S.Lenci對底端固定在彈性基礎上,頂端自由,承受軸向載荷及基礎振動的細桿的靜力學和動力學行為進行了定性分析。藉助Melnikvo函式,對混沌產生的機理進行了研究。結果表明:在不同條件下,系統混沌的產生可能是由於同宿軌道的橫截相交或2個甚至多個異宿軌道橫截相交所致。
陳立群利用Melnikvo方法,給出了準周期激勵非對稱Duffing振子存在混沌的必要條件。
D.D.Baran利用Bernoullieuler Model,Rayleigh Model和Timoshenko Model等3種數學模型分別對同一彎梁的混沌振動進行了研究,由Melinkvo函式確定的3種模型出現混沌的臨界參數值不同,即初始條件相同,在相同的外力作用下,有的模型呈現混沌,有的模型不呈現混沌。可見,對於同一個動力學系統,系統是否出現混沌行為與理論分析過程中所採用的數學模型有關,越精確的模型,其奇怪吸引子的吸引域越小。
混沌振動在工程中的利用
縱觀混沌振動研究的進展,有關其識別、機理、控制等方面的研究占的比例較大,其中有關混沌識別的文獻最多,而有關混沌振動在工程中的套用研究則剛剛起步,到20世紀末,這方面的成果還不是很多。
Li Zhe設計了混沌振動篩結構模型,從理論上分析了其混沌特性。
D.B.Logan用相關維數對滾動軸承的失效進行了診斷,他指出正常軸承振動的相關維數與內圈或外圈有毛病的軸承的相關維數不同,並根據文中所提出的計算相關維數的算法,計算出各種情況下的分維數,以診斷軸承的失效。
龍運佳設計的混沌激振器和混沌振動台是首次研製的混沌振動設備。
由於混沌振動具有比周期振動更寬的振動頻率、更大的加速度變化,有利於用作振動壓實、振動篩分、振動切削、振動落料、振動時效及寬頻振動試驗等工作。初步試驗結果表明,混沌振動篩在與傳統的單頻振動篩篩分效率相同的條件下,可節約能量。可以預言,如果用混沌振動代替傳統的單頻振動,在提高振動功效、降低能源消耗方面將會有突破性進展。