基本介紹
- 中文名:混差法
- 外文名:method of mixed differences
- 所屬學科:數學(組合數學)
- 別名:對稱重差法
- 簡介:構造BIBD設計的一種直接方法
- 提出者:玻色(R.C.Bose)
基本介紹,例題解析,相關定理,
基本介紹
下面所介紹的構作(v,k,λ)-BIBD的直接構作方法通常稱為Bose的“對稱重差法”或“混差法”。
設(X, )是一個(v,k,λ)-BIBD,它有一個m階的自同構群A,α∈A稱為設計的自同構,它變X為自身,且把
)是一個(v,k,λ)-BIBD,它有一個m階的自同構群A,α∈A稱為設計的自同構,它變X為自身,且把 變為自身,我們還假設A是可換群,運算用“+”表示,則X的元素在A作用下被非成一些軌道,設第i個元素軌道中任一固定元記為(0)i,這裡0是群的零元,當α∈A時,(0)i在自同構α作用下的象α((0)i)記作(α)i。一般地可能當α≠β時,(α)i=(β)i,此時將有A的一個子群固定(0)i。特別地,當這一固定子群為{0}時,只要α≠β,必有(α)i≠(β)i,從而第i個元素軌道恰含m個元素,另一極端情形是(0)i的固定子群為A,此時對任意α∈A,(α)i=(0)i,從而這一元素軌道只含一個元素,這樣的元素將記作
變為自身,我們還假設A是可換群,運算用“+”表示,則X的元素在A作用下被非成一些軌道,設第i個元素軌道中任一固定元記為(0)i,這裡0是群的零元,當α∈A時,(0)i在自同構α作用下的象α((0)i)記作(α)i。一般地可能當α≠β時,(α)i=(β)i,此時將有A的一個子群固定(0)i。特別地,當這一固定子群為{0}時,只要α≠β,必有(α)i≠(β)i,從而第i個元素軌道恰含m個元素,另一極端情形是(0)i的固定子群為A,此時對任意α∈A,(α)i=(0)i,從而這一元素軌道只含一個元素,這樣的元素將記作 ,或簡記作
,或簡記作 。
。









例題解析
【例1】設x={(i)j|i∈Z5,j∈Z3={1,2,3}}的加群為其自同構,群,這裡(i)j簡記為ij,這35個區組在自同構群Z5的作用下分成7個區組軌道,每個軌道中取第一個區組作為代表,則得一基底{01,12,42},{01,22,32},{02,13,43},{02,23,33},{03,11,41},{03,21,31},{01,02,03}.同一軌道中其餘區組是由第一個區組經Z5作用所得,事實上,經Z5中1的作用從每一區組可得下一個區組。



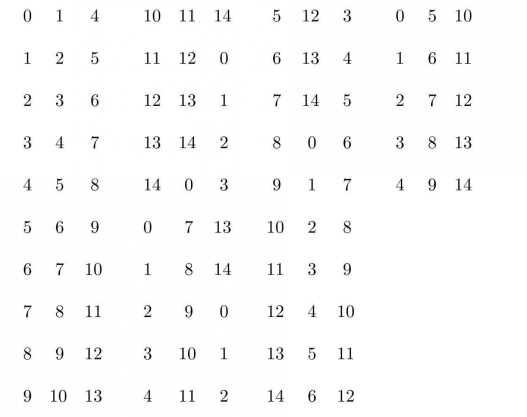
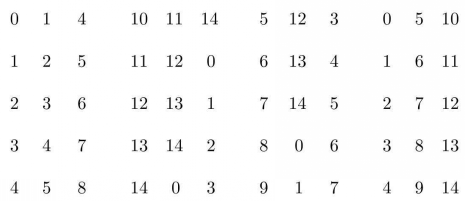
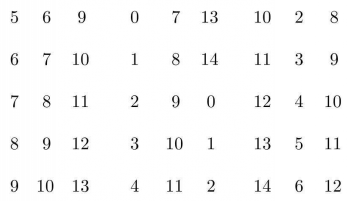
【例2】設X=Z15, 如下所示,則(X,
如下所示,則(X, )也是一個(15,3,1)-BIBD,該設計有自同構群Z15.區組軌道有三個,基底為{0,1,4},{0,7,13},{0,5,10},值得注意的是,第三個軌道較短,這是因為Z15中有3個自同構α=0,5,10能固定區組{0,5,10),即w=3,故該軌道大小為
)也是一個(15,3,1)-BIBD,該設計有自同構群Z15.區組軌道有三個,基底為{0,1,4},{0,7,13},{0,5,10},值得注意的是,第三個軌道較短,這是因為Z15中有3個自同構α=0,5,10能固定區組{0,5,10),即w=3,故該軌道大小為 ,對另外二個軌道而言,固定{0,1,4},{0,7,13}的Z15的子群為{o},故這二個長軌道大小均為15/1=15。
,對另外二個軌道而言,固定{0,1,4},{0,7,13}的Z15的子群為{o},故這二個長軌道大小均為15/1=15。



相關定理
現在從一個給定的m階可換群A出發,考慮集X=X1或X2,其中X1={(a)j |a∈A且a≠b時(a)j≠(b)j,j=1,2,...,n},X2=X1∪{( )n+1)。顯然,|X1|=mn而|X2|=mn+1,設B=
)n+1)。顯然,|X1|=mn而|X2|=mn+1,設B= 是集X的一個k元子集,{B}是若干個這樣的k元子集的族,需要有一個方法來判斷{B}是否能作為基底,使得由{B}經群A的作用而得到的所有區組的族
是集X的一個k元子集,{B}是若干個這樣的k元子集的族,需要有一個方法來判斷{B}是否能作為基底,使得由{B}經群A的作用而得到的所有區組的族 能構成一個(v,k,λ)-BIBD,其中v=|X|,為此,稱ai-at是B的(ji,jt)-差,當ji=jt時,稱之為純差;當ji≠jt時,稱之為混差,以下是這樣的一個方法。
能構成一個(v,k,λ)-BIBD,其中v=|X|,為此,稱ai-at是B的(ji,jt)-差,當ji=jt時,稱之為純差;當ji≠jt時,稱之為混差,以下是這樣的一個方法。



定理1 設可換群A,集X,X的k元子集族{B},以及 如上一段所述,如果每一個非零純差和每一個混差在由{B}中所有{B}所得的差中各出現λ次,則(X,
如上一段所述,如果每一個非零純差和每一個混差在由{B}中所有{B}所得的差中各出現λ次,則(X, )是一個(v,k,λ)-BIBD,以{B}為基底且A為其自同構群,這裡在計算次數時,如果B被A的某個w階子群所固定,A中某元素在由B所得的差中出現的次數應按實際出現次數的w分之一計算。
)是一個(v,k,λ)-BIBD,以{B}為基底且A為其自同構群,這裡在計算次數時,如果B被A的某個w階子群所固定,A中某元素在由B所得的差中出現的次數應按實際出現次數的w分之一計算。


定理2 設A是模2t+1的剩餘類環Z2t+1的加群,則以下是(6t+3,3,1)-BIBD的初始區組
{11,(2t)1,02},.,..{i1,(2t+1-i)1,02},...,{t1,(t+1)1,02},
{12,(2t)2,03},...,{i2,(2t+1-i)2,03},...,{t2,(t+1)2,03),
{13,(2t)3,01},...,{i3,(2t+1-i)3,01},...,{t3,(t+1)3,01},
{02,02,03}.
當t=2時,該定理給出的設計就是例1中的設計。
定理3 設A是剩餘類環Z3m的加群,其中m=2t+1 (mod 3),設{w,u}使得
(mod 3),設{w,u}使得

w≡u≡1(mod 3),
w+u≡0(mod m), w,u 0(mod m).
0(mod m).

當t=2時,該定理給出的設計就是例2中的設計。
以上兩個定理中自同構群均是某個剩餘類環的加群,下面將取其為某個有限域的加群A。
定理4 設v=6t+1=p,p為素數,以x記有限域CF(p)的一個原根,則存在一個(6t+1,3,1)-BIBD以A為自同構群且初始區組為