消失動量

消失動量（Vanishing Moments），在連續小波變換（Continuous Wavelet Transform），是一項非常重要的參數，用來檢視母小波（Mother wavelet）是否為高頻的函式。

基本介紹

• 中文名：消失動量
• 外文名：lost momentum

消失動量(Vanishing Moments)，在連續小波變換(Continuous Wavelet Transform)，是一項非常重要的參數，用來檢視母小波(Mother wavelet)是否為高頻的函式。

由來

在連續小波變換中，母小波有4個主要限制如下。

1. 有值區間必須是有限的(Compact Support)：

母小波不能是一個無限長的函式。

2. 必須是實函式(Real)：

因為要處理的影像不會是複數信號，且為了方便計算。

3. 偶對稱(Even Symmetric)或是奇對稱(Odd Symmetric)

4. 消失動量越高越好：

這項是最難滿足的一項。

定義

首先定義第 個動量 :

若 ，

則我們說 有 個消失動量。

如何計算消失動量

我們可以看到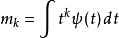 不太好計算，尤其是 很大的時候。

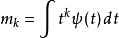
此時，可以善用傅立葉轉換來進行計算。

計算第0個動量

首先，觀察傅立葉轉換的公式:

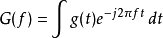
當令 時，可以看到以上公式變成:

正是第0個動量 。

因此，若要計算 的第0個動量，可以先計算 的傅立葉轉換，再取直流項(也就是 。

計算第k個動量

我們可以同樣利用傅立葉轉換來計算第 個動量。

首先，傅立葉轉換有一個性質: 在頻域微分 次，就相當於時域乘上 :

當令 時，可以看到以上公式變成:

正是第 個動量 。

因此，若要計算 的第k個動量，可以先計算 的傅立葉轉換的k次微分，再取直流項也就是 。

一些常用函式的消失動量

連續函式

哈爾小波轉換是最簡單的一種小波轉換，使用哈爾基底(Haar Basis)來做母小波。

而墨西哥帽函式(Mexican hat function)也常被用來當母小波。

哈爾基底

哈爾基底的數學表示式如下:

是一個奇函式，所以

但 是偶函式，所以

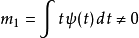
因此，哈爾基底的消失動量為1。

墨西哥帽函式

墨西哥帽函式的數學表示式:

仔細觀察， 其實是高斯函式的二次微分:

常數。

而高斯函式做傅立葉轉換仍是高斯函式:

。

利用

可以算出

。

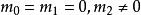
所以墨西哥帽函式的消失動量為2。

高斯函式的p次微分

墨西哥帽函式是高斯函式的二次微分，所以消失動量為2。

當

其傅立葉轉換為

。

利用

可以算出

。

所以高斯函式p次微分的消失動量為p。

連續函式的離散係數

多貝西小波(Daubechies wavelet)、Symlet 都是一些常用的離散小波，而且都是由連續小波的離散係數推導而來。

多貝西小波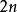 點的多貝西小波，消失動量 點的Symlet，消失動量

Symlet和多貝西小波非常類似，但是比多貝西小波還要對稱。

消失動量對於函式的意義

消失動量是用以判斷一個函式如何遞減的指標。舉例來說，對於函式

當輸入值 逐漸往無限大增加時，此函式會以 的速率遞減。 我們可用利用定義中的動量積分式 來評估此函式的遞減速率。

回到此範例中的函式，當 時，由於分子 會在 之間震盪，使得整個函式在 震盪。

此性質使得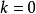 時，

函式積分式必定會收斂於0，代表第0個動量

當 時，

因此第1個動量

對於 的情況，動量積分式均會隨著 而發散。

由以上的範例，我們可藉由能夠讓動量積分式收斂為0的最大 值來判斷函式的遞減速率，而此最大{\displaystyle k}值便是函式的消失動量。

在連續小波轉換中，設計母小波的其中一個條件是有值區間比須是有限的，而母小波在有值區間內如何遞減的特性，則可由消失動量來描述。

消失動量的等價敘述

依照定義，小波母函式 有 個消失動量的條件為

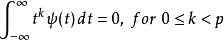
然而由於此定義中包含了一個無限範圍的連續積分，因此在設計小波母函式上並不實用。

若定義小波轉換中的尺度函式為 ，當以下小波母函式和尺度函式的關係成立時，

下列四項敘述便是等價的：

1. 小波母函式 有 個消失動量。

2. 的傅立葉轉換，以及前 次微分在 處均為零。

3. 的傅立葉轉換，以及前 次微分在 處均為零。

4. 對於 區間內的任意 值

• 是最高次方為{\displaystyle k}的多項式函式。