海特勒-倫敦近似法

由海特勒和倫敦給出的關於多粒子體系能量計算的一種近似方法。其要點是：在給出體系的哈密頓算符之後，選擇體系的恰當的近似波函式，然後用求平均值的公式計算出體系的能量。

基本介紹

• 中文名：海特勒-倫敦近似法
• 外文名：Heitler London approximation
• 套用學科：量子力學術語
• 範疇：數理科學
• 涉及：哈密頓算符
• 定義：多粒子體系能量計算的一種近似法

技術簡介

由海特勒和倫敦給出的關於多粒子體系能量計算的一種近似方法。其要點是：在給出體系的哈密頓算符之後，選擇體系的恰當的近似波函式，然後用求平均值的公式計算出體系的能量。

1927年德國物理學家W.H.海特勒和F.W.倫敦首次完成了氫分子中電子對鍵的量子力學近似處理，這是近代價鍵理論的基礎。

海特勒-倫敦近似法處理氫分子

氫分子的哈密頓算符是：

式中、為核、與電子之間的距離；為兩個電子之間的距離；為兩個原子核之間的距離(圖1)；

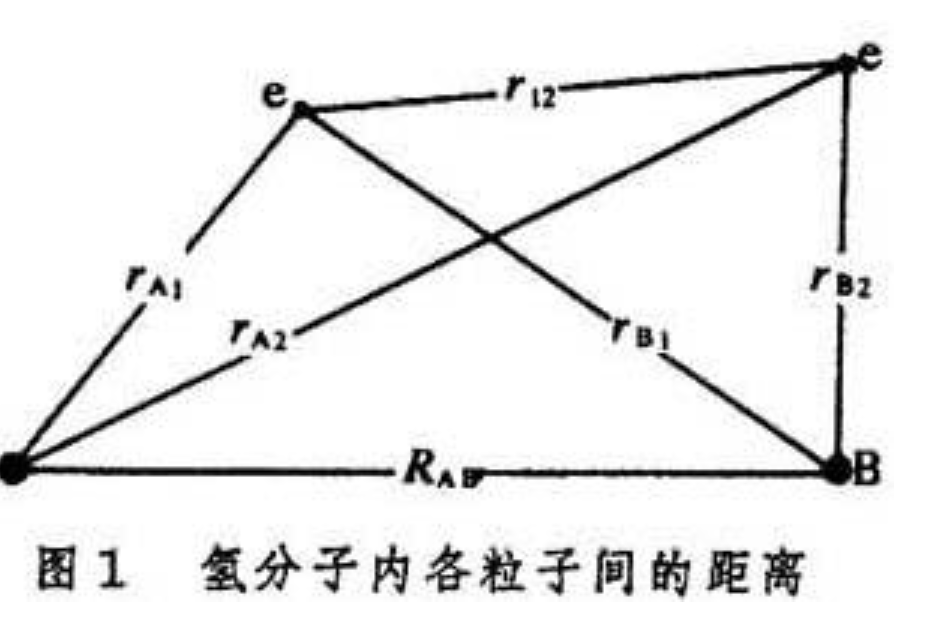
圖1 氫分子內個粒子間的距離

表示兩個原子核之間的勢能(氫核和電子電荷皆為基本電荷單位)；、、、、也是勢能；是拉普拉斯算符。

海特勒－倫敦方法的要點在於如何恰當地選取基態的近似波函式(或稱嘗試波函式)，然後用變分公式使氫分子能量為最低(假定是歸一化的)：

式中表示複數共軛。考慮兩個氫原子組成的體系，若兩個氫原子(有電子)和(有電子)的基態波函式為：

假如兩個氫原子相距很遠，那么體系波函式是：

實際上兩個電子是不可區分的。同樣合適的函式是：

兩個函式和都對應相同的能量。海特勒和倫敦就取兩個函式的等權線性組合作為的變分函式：

解久期方程得，波函式和能量是：

式中，

稱原子軌道的重疊積分。算出能量公式中各項，積分得：

式中、、都是的函式。若用表示分子能量與兩個分離原子能量之差(圖2)：

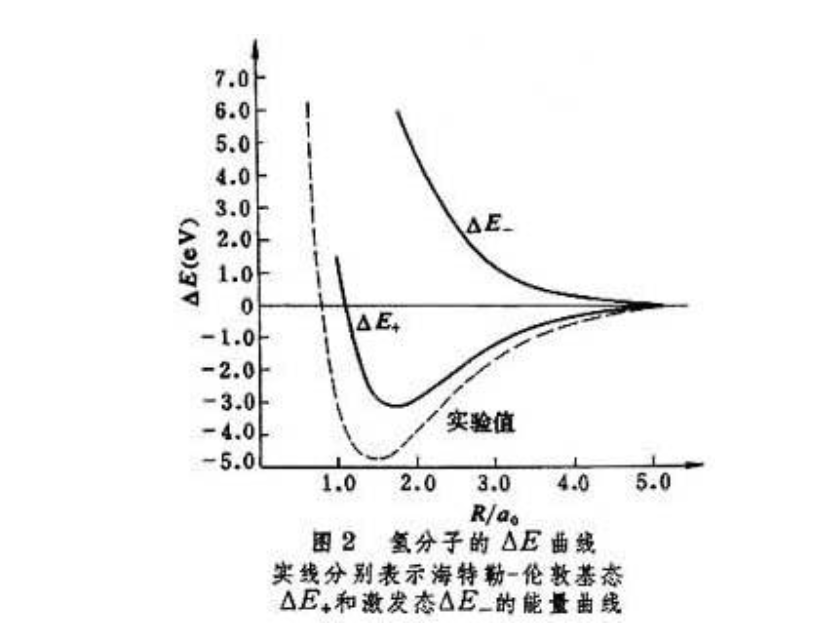
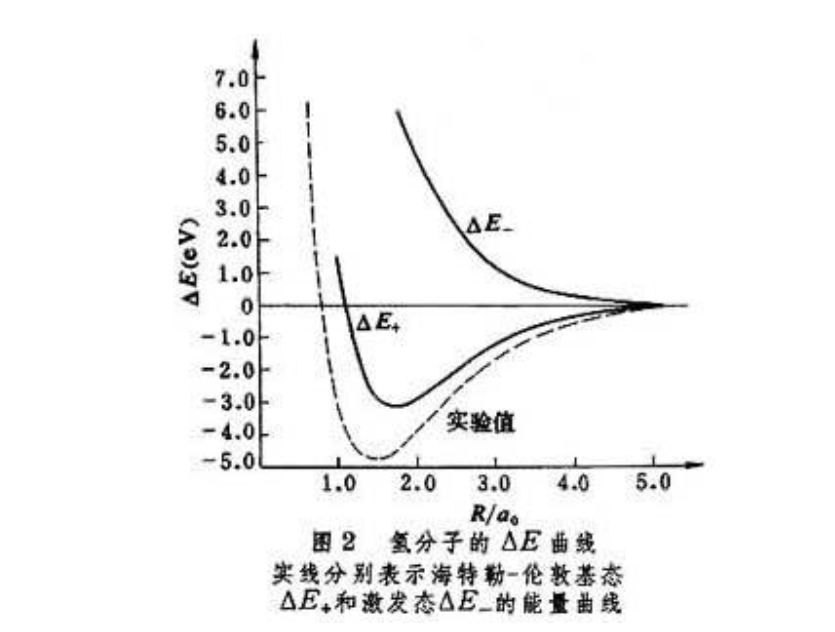
圖2 氫分子的E曲線

就是分子相對於分離原子能量為零時的能量。因為和都是負量，態比態能量更低，圖2 中曲線總處於曲線的下面。圖2中虛線表示實驗勢能曲線。 曲線有極小值，表示形成了穩定的。在平衡核間距 R_e=0.87埃，計算得到離解能D_e=3.14電子伏(或稱結合能)。與實驗值R_e=0.742埃，D_e=4.75電子伏略有差異，這反映了海特勒－倫敦法的近似程度。在減小時一直升高。稱海特勒-倫敦函式，描述基態，描述排斥態。