海丁謂詞演算公理系統是由海丁(Heyting, A.)於1934年建立的.該系統是直覺主義邏輯的形式化,它反映了在直覺主義框架中數學思維的邏輯規律.
海丁謂詞演算公理系統(Heyting axiomatic system of predicate calculus)謂詞演算的一種公理系統.它是由海丁(Heyting, A.)於1934年建立的.該系統是直覺主義邏輯的形式化,它反映了在直覺主義框架中數學思維的邏輯規律.這個系統實際上是在英國數理邏輯學家羅素(Russell,B. A. W. 和英國邏輯學家、數學家懷特海(Whitehead, A. N.)的系統基礎上修改而成.在海丁系統中,排除了羅素和懷特海系統中所有表達排中律的命題以及以這些命題為基礎的命題.與羅素一樣,海丁在定理前加上一個斷定號“卜”.與羅素不同的是,海丁在公理前加上兩個斷定號“卜卜”.海丁系統的命題演算部分的公理共有十一條:
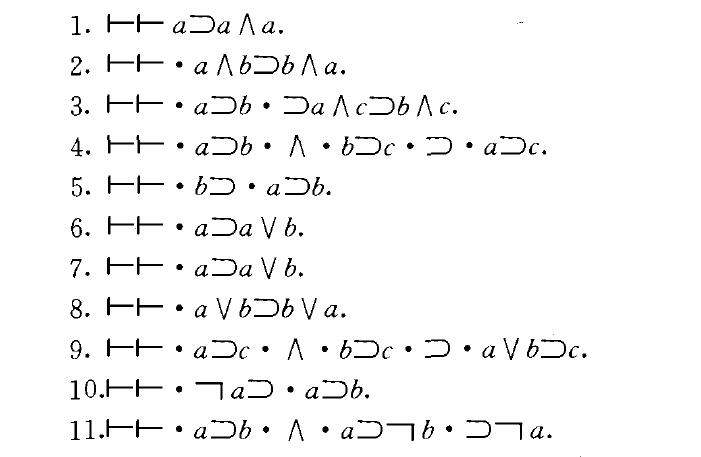
在上述公理中,海丁引用了一個新的否定詞符號“門”,以區別於在他以前通常使用的否定詞符號 “一”.他之所以這樣做,是因為直覺主義的否定與通常的否定意義有很大不同.例如,在羅素和懷特海的系統中,命題:

均為定理.但在海丁的系統中,命題1是定理,命題2不再是定理. 為了建立謂詞演算,海丁引進全稱量詞(以符號,’(x)”表示)和存在量詞(以符號“(Ex)”表示),並且添了兩條公理:
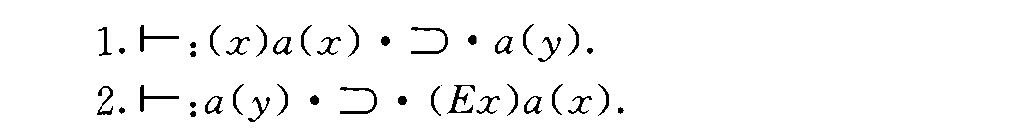
海丁認為,藉助於命題演算和謂詞演算能重建整個算術.然而,他又認為,只有將這些命題和運算的內容的實際意義記在心頭,這種重建才真正可能.
