波波夫穩定判據

定義

在頻率域內，由系統的線性部分的頻率特性直接分析非線性單變數系統穩定性的判據。使用這樣的判據分析非線性系統穩定性的方法稱為波波夫法，它僅適用於能將系統中的非線性和線性部分分開的非線性系統。

設非線性系統如圖1所示。系統中非線性特性y=f(x)可具有任意形式，但必須滿足下列條件

式中x為非線性部分的輸入;f(x)為非線性部分的輸出;k1，k2為將非線性特性f(x)夾在中間的兩條直線的斜率，k2可為任意正值或無窮大，要求k1≥0。

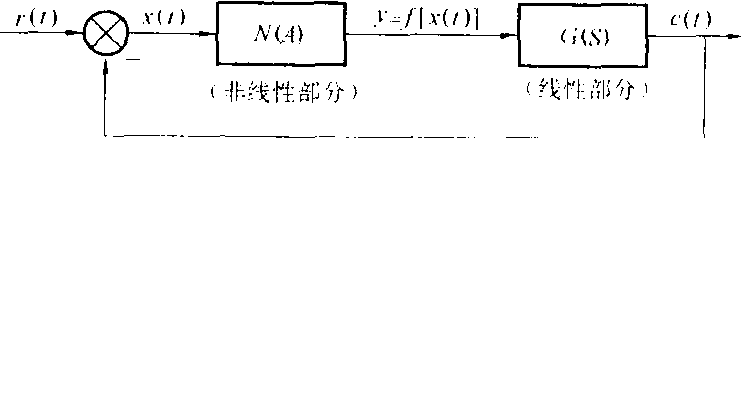
圖1 非線性系統

設非線性系統中線性部分的全部極點具有負實部，其頻率特性為G(jω)，再令

式中

則作為波波夫穩定判據的非線性控制系統大範圍漸近穩定的充分條件為

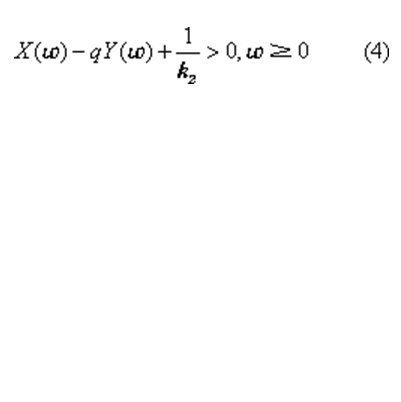
式中 q為某有限數。

如果令

則式(5)代表一條在G*(jω)平面上通過點(-1/k2，j0)，斜率為1/q的直線，稱此線為波波夫直線，如圖2中的直線(1)。

若系統的G*(jω)軌跡線，對於所有ω≥0，均位於波波夫直線右側，則此非線性系統為大範圍漸近穩定的。

圖2 波波夫穩定判據圖解之一

通過G*(jω)軌跡線和負實軸的交點作與G*(jω)相切的切線，如圖2中直線(2)。如果整個G*(jω)軌跡線位於此切線右側，則由此切線表示的波波夫直線將給出保證系統大範圍漸近穩定時的最大k₂值。

由於G*(jω)軌跡線的形狀不同，q的數值可以為q>0，或q<0，或q=0。

如果非線性系統中線性部分的極點中有一個為零，其他極點都具有負實部，則為使該系統大範圍漸近穩定，除應滿足式(1)和式(4)外，還應滿足

式中 resG(s) |s=0為G(s)在s=0處的留數。

如果非線性系統線性部分的G (jω)軌跡線在複平面上不包圍下面定義的圓，也不和圓相交，則非線性系統是大範圍漸近穩定的。圓的方程為

式中 X、Y分別為G(jω)平面實軸和虛軸上的變數。

如果非線性特性的k1=0，則上述圓的圓心坐標和圓的半徑都將趨向無窮大。這樣，圓的方程將變為通過點(-1/k2，j0)、斜率為1/q=∞的直線方程，即

此時，波波夫直線便是通過點(-1/k2，j0)、斜率1/q=∞的直線，如圖3所示。

圖中，G1(jω)曲線(1)對應於系統是大範圍漸近穩定的，G2(jω)曲線(2)對應於系統是不穩定的。

①適用範圍有限制[如式(1)所示];

②可以套用於高階系統，這點要比相平面法優越;

③是一個準確判定穩定性的方法，這點比描述函式法優越;

④具有類似使用奈奎斯特穩定判據的方法的優點，很適合工程套用。只是，奈奎斯特穩定判據是充分必要條件，而波波夫穩定判據是充分條件。

圖3 波波夫穩定判據圖解之二