法方程是測量平差計算中的一個重要的方程,是由平差函式模型線性化後的方程式、以及在VTPV=min的條件下所導得的方程式合併而成的聯立方程組。
基本介紹
- 中文名:法方程
- 外文名:Fa Fangcheng
- 類屬:測量平差計算
- 屬性:方程式
- 領域:數學
概念
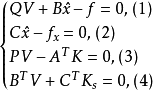
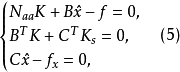
秩虧網平差



法方程是測量平差計算中的一個重要的方程,是由平差函式模型線性化後的方程式、以及在VTPV=min的條件下所導得的方程式合併而成的聯立方程組。
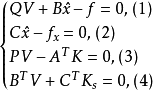
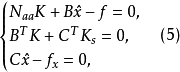


法方程是測量平差計算中的一個重要的方程,是由平差函式模型線性化後的方程式、以及在VTPV=min的條件下所導得的方程式合併而成的聯立方程組。...
“平面方程”是指空間中所有處於同一平面的點所對應的方程,其一般式形如Ax+By+Cz+D=0。...
通過上述方法得到的三彎矩方程,便於在數學上求解(見變形分配法)。 中文名:連續梁 外文名:continuous beam 拼音:lianxuliang 釋義:有三個或三個以上支座的梁 簡稱...
切線法是通過曲線上的一些特徵點的切線的交點坐標關係來計算磁性體的產狀。...... 切線法方程求根方法 編輯 切線法又稱為牛頓法,是一種一般情況下具有二階收斂速度...
極坐標法是在控制點上測設一個角度和一段距離來確定點的平面位置。...... 極坐標法方程 編輯 用極坐標系描述的曲線方程稱作極坐標方程,通常表示為r為自變數θ的...
自洽場方法(self-consistent field method, SCF),即自洽場近似法,是量子力學中疊代求解多粒子系統薛丁格方程的基本方法。其基本思想是首先按照某種方法給出波函式的...
問題,線性方程組的直接解法與疊代解法,數值逼近方法,數值微積分,非線性方程疊代...3.3.1 (線性)最小二乘問題的法方程3.3.2 正交化算法第4章 數值積分和...
教材主要介紹計算機上求解各種數值問題的常用基本值方法及其算法設計,包括解線性方程組的直接法,插值法與最小二乘法,數值積分與微分、常微分方程數值解法,逐次逼近法...
銣-鍶法是一種地質計時方法,是根據87Rb經β-衰變形成穩定的87Sr的規律而建立的。...... 等時法線方程為 (Sr/Sr)- (Sr/Sr)=(Rb/Sr)(e-1) 其中(Sr/Sr...
