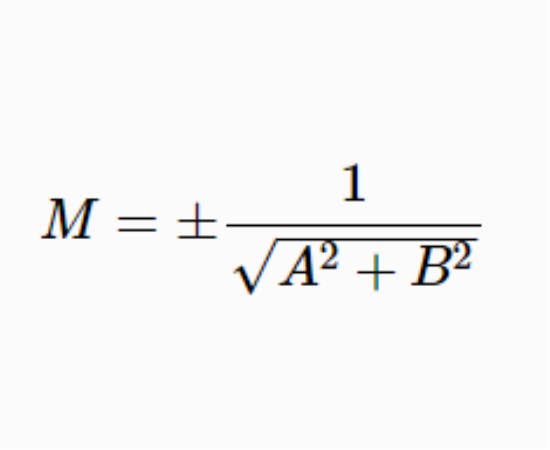法化因子

如要將直線方程的一般式Ax+By+C=0(A²+B²≠0)化為法線式xcosα+ysinα-p=0，只須將一般式乘以一個常數因子M，因子M即稱法化因子(normal factors)，M的正負號按下列法則確定：(1)C≠0時，與C異號；(2)C=0，而B≠0時，與B同號；(3)B=C=0時，與A同號。

基本介紹

• 中文名：法化因子
• 外文名：normal factors
• 所屬學科：數學
• 所屬問題：平面解析幾何
• 簡介：將直線方程化為法線式所乘的常數
• 相關概念：法化問題，法化方程

基本介紹

法化因子是一個常數，指將直線方程化為法線式所乘的常數。將直線方程的一般式Ax+By+C=0乘以常數

即可得到這條直線的法線式方程

常數 稱為該直線的法化因子。它的“±”號的取法是：

1.當C≠0時，λ和C異號；

2.當C=0，B≠0時，λ和B同號；

3.當C=0，B=0時，λ和A同號。

直線的法化方程——從點到直線的距離

方程Ax+By+C=0乘上法化因子以後所得到的方程

叫作直線Ax+By+C=0的法化方程，把點(x，y)的坐標代入直線的法化方程的左邊，所得結果的絕對值等於從這個點到直線的距離h(x,y)：

直線法化因子的證明

考慮在直線坐標中直線方程的法化問題。

引理向量(A，B)垂直於由方程

表示的直線。

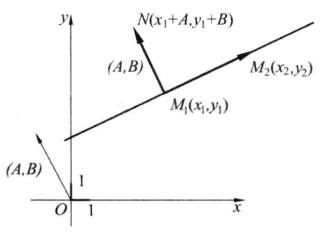圖1

證明 在直線（1）上取任意兩個不同的點 和 (圖1),於是有

和

從第二個等式減去第一個,我們得到

這等式的左邊表示向量(A,B)和 的數量乘積。因此。這數量乘積等於零。而這就是說。向量(A,B)垂直於向量 ，因此，也垂直於直線（1）。

現在我們約定取法化因子的正負號與自由項C的正負號相反。

定理 在直角坐標系統中，方程（1）的法化因子等於 (其正負號由剛才說的約定決定)。

證明 在直線（1）上取點 ，再把向量(A,B)放在這個點上(圖1)，向量終點N的坐標將為, (它是向量 的終點, 是向量 和 的和)。把這些坐標代人方程（1）的左邊，並且考慮到 ，我們得到

在左邊乘上所求的法化因子λ，我們應該得到從點N到直線（1）的距離，但是從引理看到，這距離等於向量(A，B)的長度，即 。這樣,我們有

由此

故定理得證。