一個函式的赫爾德指數反映了函式的正則性,即光滑性。小波變換的一個重要性質就是可以刻畫函式的正則性。
基本介紹
- 中文名:正則性刻畫
- 外文名:characterization of regularity
- 適用範圍:數理科學
簡介,赫爾德連續性,小波變換,
簡介
一個函式的赫爾德指數反映了函式的正則性,即光滑性。
小波變換的一個重要性質就是可以刻畫函式的正則性。具體表述為:如果ψ(x)是一個具有緊支集的小波,設f(x)∈L2(R)有界並且連續,那么若且唯若存在常數C>0,使

赫爾德連續性
赫爾德連續性是刻畫函式光滑程度的一個概念。
如果對函式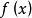 ,存在常數
,存在常數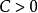 ,使對任意
,使對任意 ,有
,有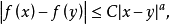 那么稱函式
那么稱函式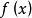 是
是 (
(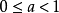 )次赫爾德連續的,並稱
)次赫爾德連續的,並稱 為赫爾德指數。
為赫爾德指數。
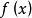
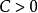

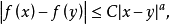
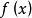

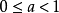

小波變換
(wavelet transform,WT)
小波變換是一種新的變換分析方法,它繼承和發展了短時傅立葉變換局部化的思想,同時又克服了視窗大小不隨頻率變化等缺點,能夠提供一個隨頻率改變的“時間-頻率”視窗,是進行信號時頻分析和處理的理想工具。
它的主要特點是通過變換能夠充分突出問題某些方面的特徵,能對時間(空間)頻率的局部化分析,通過伸縮平移運算對信號(函式)逐步進行多尺度細化,最終達到高頻處時間細分,低頻處頻率細分,能自動適應時頻信號分析的要求,從而可聚焦到信號的任意細節,解決了Fourier變換的困難問題,成為繼Fourier變換以來在科學方法上的重大突破。
