歐拉閉跡

圖G的頂點與邊的交錯序列：v0e1v1e2v2…vl-1elvl(l>0)，其中ei+1(i=0,1,…,l-1)的端點是vi與vi+1，且i≠j時，ei≠ej(1≤i,j≤l)，叫做圖G的跡，如果v0與vl重合，則稱為閉跡。通過圖G的所有邊的（閉）跡，稱為歐拉（閉）跡。

基本介紹

• 中文名：歐拉閉跡
• 適用範圍：數理科學

背景

歐拉閉跡圖論的第一篇論文是著名數學家歐拉於1736年發表的，這篇論文對當時舉世矚目的數學難題——哥尼茨堡七橋問題作出了否定的答案。

哥尼斯堡（Konigsberg）是現在俄羅斯的加里寧格勒，該城位於普瑞格爾（Pregel）河畔，城區由兩岸及河中的兩個小島四個區A，B，C，D組成，全城由七座橋相連，如圖所示。

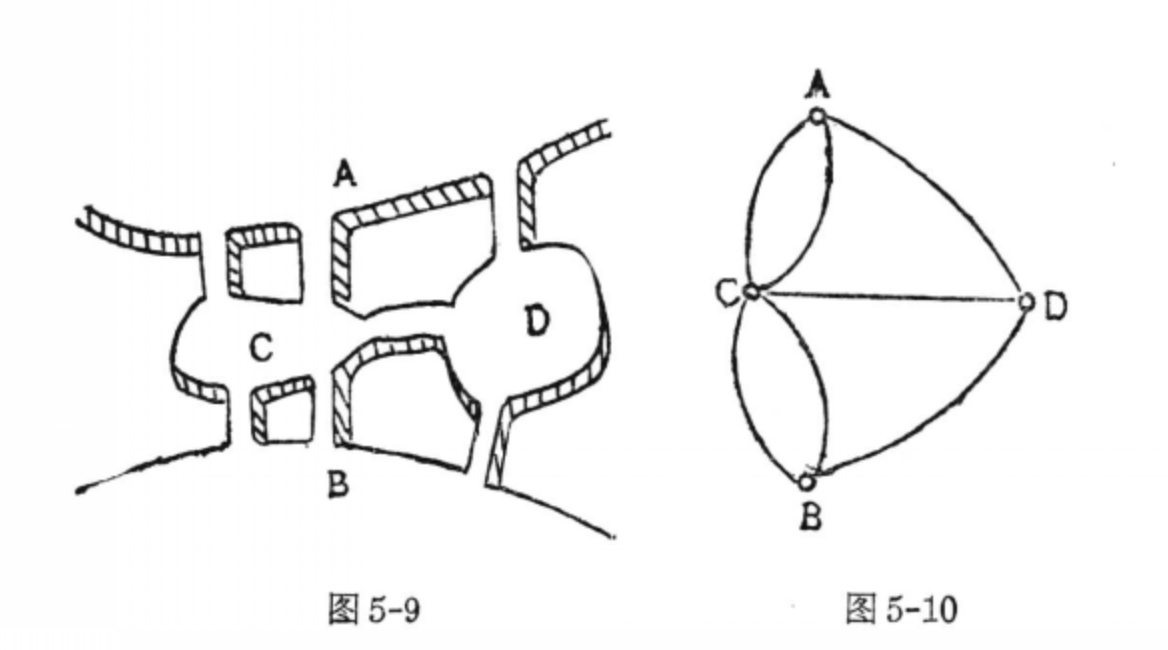圖1

當時城中居民熱衷於這樣一個問題：遊人從城中某一地點出發，能否行遍七座橋各1次而回到原地？問題看來並不複雜，但誰也解決不了。於是有人就去請教歐拉。歐拉把四塊陸地抽象成4個點，每座橋抽象成連線兩點的線段，而得到右下圖。從而問題就變成：從某一頂點出發，能否不重複地行遍所有的邊而回到這個頂點？

如果答案是肯定的，那么圖中各邊連線的每個頂點，既有“進入”這個點的邊，又有“走出”這個點的邊。就是說每個頂點必須是偶次點。但右圖四個頂點都是奇次點，所以答案是否定的。

定義

跡和閉跡

圖G的頂點與邊的交錯序列：v₀e₁v₁e₂v₂…v_l-1e_lv_l(l>0)，其中e_i+1(i=0,1,…,l-1)的端點是v_i與v_i+1，且i≠j時，e_i≠e_j(1≤i,j≤l)，叫做圖G的跡，如果v₀與v_l重合，則稱為閉跡。

歐拉閉跡

通過圖G的所有邊的（閉）跡，稱為歐拉（閉）跡。

定理

設G是一個連通圖，則

（1）G是歐拉閉跡的充要條件是G中有且僅有兩個奇次頂點；

（2）G是歐拉閉跡的充要條件是G中全是偶次頂點。

推論

一個能夠一筆畫的圖，就是有歐拉跡或歐拉閉跡的圖；反之，一個有歐拉跡或歐拉閉跡的圖，必是能一筆畫的圖。根據上面的定理，我們有推論：設G是一個連通圖。則圖G能一筆畫的充要條件是G中沒有奇次頂點或有且只有兩個奇次頂點。