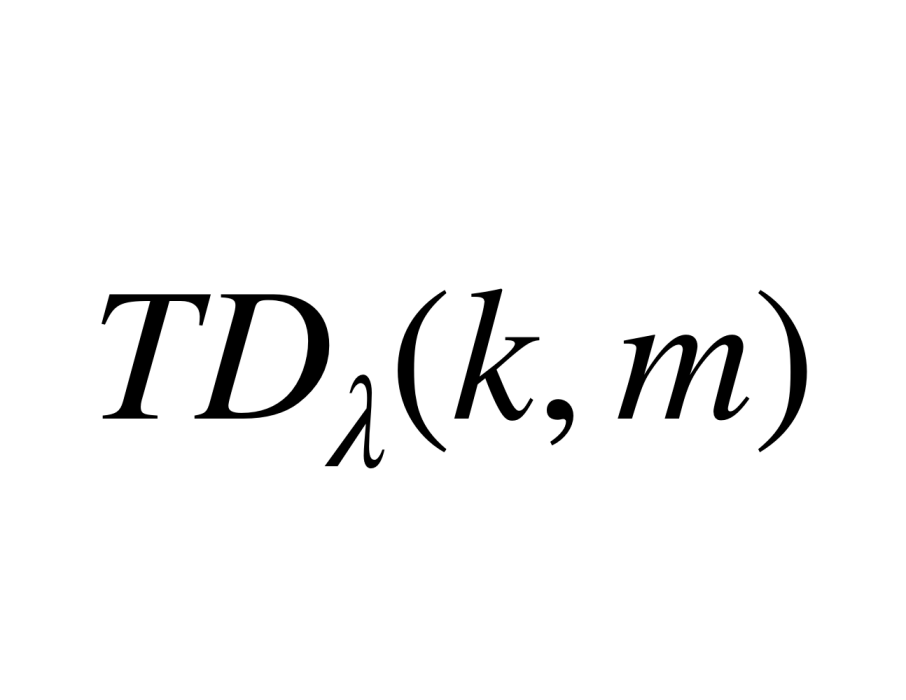基本介紹
- 中文名：橫截設計
- 外文名：transversal design
- 適用範圍：數理科學
- 釋義：組的大小全相等且組的個數與區組大小相同的可分組設計
簡介,可分組設計,
簡介
橫截設計是一類特殊的可分組設計。即組的大小全相等且組的個數與區組大小相同的可分組設計。
設組的大小為m且區組大小為k，屬於不同組的兩個元恰含於λ個區組，這樣的橫截設計記為
。當λ=1時，
簡記作
。
由於的存在性等價於k-2個m階互相正交拉丁方的存在性，橫截設計的遞推構造方法為正交拉丁方的構造提供了有力的工具。橫截設計在其他類型的組合設計的構造中也很有用。
可分組設計
[group divisible design]
設v，λ為給定的正整數，K，M 為給定的正整數集。設D= (𝑋,𝒢,ℬ).其中X為一個v元集，𝒢構成𝑋的一個劃分，且|𝒢|> 1，ℬ是X 的一個子集族。𝒢的元素叫做組(group)，B的元素叫做區組(block)。若下述條件滿足:
(1)對任意B∈ℬ，都有|BI∈K；
(2)對任意G∈𝒢，都有|G|∈M；
(3)對任意B∈ℬ與任意G∈𝒢，都有|B∩G|≤1；
(4)X中任意一對屬於不同組的元素恰好同時包含在λ個區組中，
則稱D為一個可分組設計，記作GDD[K,λ,M;v]可或簡記為(K,λ)–GDD。v 叫做設計的階，λ叫做相遇數。若𝒢包含
個大小為
的組，i=1，2，...，s，且
，則稱D是型為
的(K,λ)–GDD。
當K={k}時，把(K,λ)–GDD簡記作(k,λ)–GDD。如果λ=1,則(K，λ)-GDD簡記作K-GDD。當 M={m}時，則稱(K,λ)–GDD為均勻(uniform)可分組設計。
威爾遜基本構作法(Wilson's fumdamental construction)是組合設計理論中最重要的遞歸構作法之一，可分組設計在威爾遜基本構作法中充當著主導設計(master design) 的作用。
