橢圓型反演變換:基本介紹,相關介紹,相關定理,

橢圓型反演變換(elliptic inversion transformation)是反演變換的一，指反演冪k<0的反演變換。根據反演變換的定義及任何一個實數的平方不會是一個負數，橢圓型反演變換不存在二重點。

基本介紹

中文名：橢圓型反演變換
外文名：elliptic inversion transformation
所屬學科：數學
所屬問題：幾何變換
簡介：反演冪k

基本介紹,相關介紹,相關定理,

基本介紹

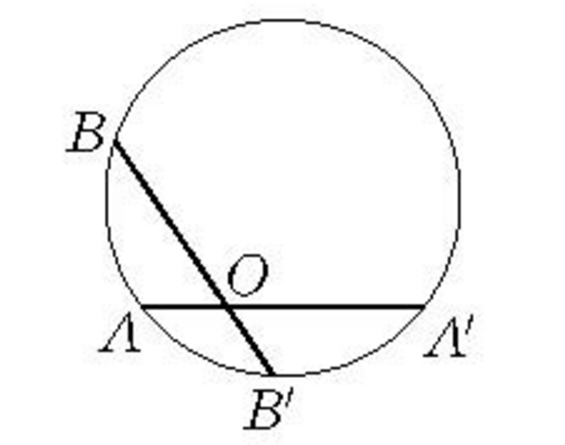
當共線三點A，O，A確定一個橢圓型反演變換時，對任一點B，均可用幾何作圖求出其反演點B′，當A，A′，B不共線時，過該三點作圓，此圓與直線OB的第二交點B′即為B的反演點(如圖1)；當A，A′，B共線時，可按比例第四項作圖，求出OB′的長以確定B′點。

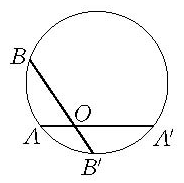
圖1

定義1 設O是平面π上的一個定點，k是一個非零常數。如果平面π的一個變換，使得對於平面π上任意異於O的點A與其像點A' ，恆有

(1)A'、O、A三點共線；

(2)

，

則這個變換稱為平面π的一個反演變換，記作I(O,k)，其中定點O稱為反演中心，常數k稱為反演冪，點A'稱為A的反點。當反演冪k> 0時，反演變換I(O,k)稱為雙曲型反演變換；當k < 0時，反演變換I(O,k)稱為橢圓型反演變換，顯然，當點A'是點A的反點時，點A也是點A'的反點，因而點A與A'互為反點。由此可見，反演變換是可逆的，且其逆變換就是自身。

相關介紹

從反演變換的定義可以看出，反演中心在普通平面上不存在反點，除此之外，平面上其他的任意一點都存在唯一的一個反點。因此，嚴格地講，“反演變換”不是平面π的一個變換，而只是平面π的一個“擬變換”(因為有一個點沒有像)，但如果將平面π去掉反演中心，則“反演變換”仍是這個有“洞”的殘缺平面的一個一一變換。

在反演變換I(O,k)下，如果平面π的圖形F的像為圖形F'，則圖形F'稱為圖形F關於反演變換I(O,k)的反形，簡稱圖形F'是圖形F的反形。

顯然，在反演變換下，如果圖形F'是圖形F的反形，則圖形F是圖形F'的反形，因而圖形F與圖形F'互為反形。

反演變換的不動點稱為自反點；而反演變換的不變圖形則稱為自反圖形。

如果反演變換I(O,k)是一個雙曲型反演變換，即反演冪k>0，令

，則以反演中心O為圓心、r為半徑的圓稱為反演變換I(O,k)的反演圓，而r則稱為反演半徑。

如果反演變換I(O,k)是一個橢圓型反演變換，即反演冪k<0，令

,則以反演中心O為圓心、r 為半徑的圓也稱為反演變換

的反演圓，r則稱為反演半徑。

無論是雙曲型反演變換，還是橢圓型反演變換，它們都有一個反演圓，圓心為反演中心，當反演冪為k時，反演半徑為

。且由反演變換的定義知，反演圓是反演變換的自反圓；雙曲型反演變換的反演圓上任意一點都是自反點；橢圓型反演變換的反演圓上任意一點都變為這一點的對徑點(以這一點為一端點的直徑的另一端點)；橢圓型反演變換沒有自反點；反演圓內的點(除圓心外)的反點在反演圓外，而反演圓外的點的反點則在反演圓內(圖2、圖3)。