在數學和計算機科學中,機率自動機(Probabilistic Automaton,PA)是非確定性有限自動機的推廣; 它包括給定轉換到轉換函式的機率,將其轉換為轉換矩陣。 因此,機率自動機概括了馬爾可夫鏈或有限類型的子移位的概念。 機率自動機識別的語言稱為隨機語言; 這些包括常規語言作為子集。 隨機語言的數量是不可數的。
基本介紹
- 中文名:機率自動機
- 外文名:probabilistic automaton
- 縮寫:PA
介紹
定義


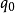


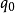
































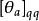









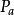
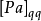



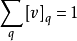






在數學和計算機科學中,機率自動機(Probabilistic Automaton,PA)是非確定性有限自動機的推廣; 它包括給定轉換到轉換函式的機率,將其轉換為轉換矩陣。 因此,機率自動機概括了馬爾可夫鏈或有限類型的子移位的概念。 機率自動機識別的語言稱為隨機語言; 這些包括常規語言作為子集。 隨機語言的數量是不可數的。


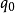


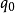
































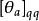









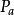
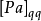



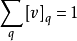






在數學和計算機科學中,機率自動機(Probabilistic Automaton,PA)是非確定性有限自動機的推廣; 它包括給定轉換到轉換函式的機率,將其轉換為轉換矩陣。 因此,機率自動機...
機率自動機論(probabilistic automata theory)自動機論的次級學科,主要研究所處環境或內部具有(有限或無限的)隨機因素的自動機。與非機率型自動機不同之處,是機率...
計算機控制系統的控制程式具有有限狀態自動機(FA)的特徵,可以用有限狀態機理論來描述。有限自動機(Finite Automata Machine)是計算機科學的重要基石,它在軟體開發領域...
反機率接收機是指建立在反機率準則墓礎上對目標進行檢測的接收機。反機率準則是建立在機率論中貝葉斯法則的基礎上,要求事先知道信號加噪聲本身出現的機率(從實踐中...
自動機論是研究離散數字系統的功能和結構以及兩者關係的數學理論。可分為有限自動機論、無限自動機論、機率自動機論、細胞自動機論、抽象自動機論 五個次級學科。....
自動機理論是一種將離散數學系統的構造,作用和關係作為研究對象的數學理論。在理論計算機科學中,自動機理論是對抽象機和它們能解決的問題的研究。自動機理論密切關聯...
抽象自動機是—種能夠識別語言的抽象裝置,它不是具有物理實體的機器,而是表示計算機運算方式的抽象的邏輯關係系統,這樣的抽象自動機可以用來檢驗輸入的符號串是不是...
在計算理論中,非確定有限狀態自動機或非確定有限自動機(NFA)是對每個狀態和輸入符號對可以有多個可能的下一個狀態的有限狀態自動機。...
隨機賦時狀態自動機(stochastic timed state automaton )狀態自動機概念的一種擴充.其定義為六元組(},.%},r} p} po}G>,其中f為可數的事件集;虎為可數的...
元胞自動機(cellular automata,CA) 是一種時間、空間、狀態都離散,空間相互作用和時間因果關係為局部的格線動力學模型,具有模擬複雜系統時空演化過程的能力。...
《形式語言,自動機理論與計算導論》是2012年2月1日由電子工業出版社出版的圖書,作者是卡馬拉(Kamala Krithivasan)、拉瑪(Rama R),譯者是孟宇龍、李健利、王宇華...
《物理系統的元胞自動機模擬》是清華大學出版社出版的圖書,作者是肖帕爾。本書論述深入淺出,並附有大量習題,非常適合於用作物理學領域的研究生教材,同時可供從事...
1.8.1概述1.8.2有限狀態自動機1.8.3機率自動機1.8.4細胞自動機1.9圖靈機1.10心智的計算理論第2章心智模型CAM2.1概述2.2心智建模標準2.3認知心智建模...
