機率籃球棋

《機率籃球棋》遊戲系列是伍小強博士自1992年起歷經十多年研發，創作而成的中國原創的創意文化作品和產品。自近幾年推廣以來深受廣大籃球及遊戲愛好者的喜愛。

基本介紹

• 中文名：機率籃球棋
• 類型：遊戲
• 研發人：伍小強
• 開始研發時間：1992年

介紹

《機率籃球棋》遊戲系列是伍小強博士自1992年起歷經十多年研發，創作而成的中國原創的創意文化作品和產品。自近幾年推廣以來深受廣大籃球及遊戲愛好者的喜愛。它有實物，電腦及網路等遊戲形式，其中融合了象棋，圍棋，麻將，撲克，色子等棋牌遊戲文化元素，籃球運動的體育文化元素，以及機率數學，軟體設計等科技元素。它以棋遊戲的形式模擬籃球運動比賽，適合一人消遣，兩人至十人團隊對抗比賽及觀賞。該遊戲結合了比賽技巧及機率運氣特徵，其規則運用了發明者為此而研發的“組合餘數隨機生成”的方法科學及公正地決定遊戲中各種機率事件的運氣。

研發過程

《機率籃球棋》遊戲系列是伍小強博士自1992年起歷經十多年研發，創作而成

的中國原創的創意文化作品和產品。自近幾年推廣以來深受廣大籃球及遊戲愛好者的喜愛。它有實物，電腦及網路等遊戲形式，其中融合了象棋，圍棋，麻將，撲克，色子等棋牌遊戲文化元素，籃球運動的體育文化元素，以及機率數學，軟體設計等科技元素。它以棋遊戲的形式模擬籃球運動比賽，適合一人消遣，兩人至十人團隊對抗比賽及觀賞。該遊戲結合了比賽技巧及機率運氣特徵，其規則運用了發明者為此而研發的“組合餘數隨機生成”的方法科學及公正地決定遊戲中各種機率事件的運氣。

機率籃球棋

發明人簡介

伍小強博士在中國科學院研究生院講課

伍小強博士1983年畢業於北京大學力學系，1989年獲美國洛杉磯加州大學工程博士，之後在美國加州及矽谷各高科技公司從事技術及管理工作，先後任職於Microsoft, IBM, FileNET, Autodesk 等著名IT企業。伍博士於2003年回國工作和創業，從事IT諮詢，軟體開發，IT教學及培訓的工作。伍博士

回國前是矽谷西北理工大學的兼職教授，自2002年起為中國科學院研究生院的客座教授，是資深的IT教學及培訓專家。

機率籃球棋

推廣活動

“強方杯”北京市小學生五子棋團體邀請賽(2008.11)	藝黠女士（左），主辦單位，五子棋女子全國冠軍。; 伍小強（中），贊助單位，《機率籃球棋》發明者。; 房樹文老師（右），主裁判，中國棋院青少年培訓競賽副主任，高級教練，《盲人五子棋》發明者。
清華附小棋藝班(2008.6)	清華附小棋藝班(2008.5)
迎奧運北京高校中國象棋邀請賽(2008.5)	珠海高校棋類聯賽(2008.5)
中國大學生《機率籃球棋》俱樂部聯盟(2008.3)	中國大學生《機率籃球棋》俱樂部聯盟(2007.12)
珠海國際學校(2008.1)	揚州市少年宮(2007.10)
上海美國學校(2007.4)	珠海市小學生課外活動(2007)

遊戲規則

新手入門(投球練習)

機率籃球棋

新手入門：

最好的入門方法是由教練或熟練的玩家示範講解遊戲方法及規則，並且帶著練習。觀看別人比賽也是很好的方法。自己學可以參考遊戲規則。可以觀看錄影或多媒體培訓資料。也可以通過電腦遊戲版學(電腦會自動引導和提示您)。一般來說，在有教練教的情況下，1分鐘之內就可進行投球練習，3到5分鐘之內就可使用初級規則進行比賽。10多分鐘之內就可使用中級規則。

級別：

初學者可以先從投球練習開始，然後學習使用初級規則進行比賽，直到中級和 高級規則。高級別的規則可以替換低級別的規則，如：中級的直傳球和拋球可以替換初級的簡單傳球規則。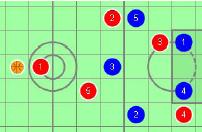

機率籃球棋

投球練習：

隨意把球員棋子放在球場格子上，把球放在自由球員的鄰居，讓該球員投球。

兩分或三分球：

若投手站在三分線內，即使球在三分線外，則是投兩分球。若投手站在三分線外，即使球在三分線內(如圖1)，則是投三分球。進球機率：機率由籃球的位置以及防守的情況決定。

圖1. 三分球，60%機率

未被防守的投球：

進球的機率取決於籃球與籃框的距離。扣籃(球在籃框的位置上，如圖2)的概 率為100%。球每遠離籃框一格機率減10%。三步上籃(球在籃框的鄰居，如圖3)的機率為90%。如此類推。三分球最高的機率為60%(如圖1)。球的位置如果在籃板的後面(第0行)，則機率為零。 圖2. 扣籃，100%機率

機率籃球棋

圖3. 三步上籃，60%機率

對投球的防守：

若投手或籃球的鄰居有防守隊員，則投手或籃球被防守。被防守的投球：投手每被一人防守機率減10%。球每被一人防守減20%。 例如：圖3的投球情景。紅3號投球。進球的機率為90%-10%(藍5號防投手)-20%(藍1號防籃球)=60%

運氣：

裁判和參賽者可以用各種機率工具(如撲克牌，色子)及“組合餘數”的方法決定 某一機率事件的運氣及結果。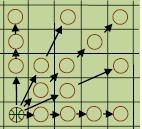

機率籃球棋

使用撲克牌：

把一付撲克牌的大，小王，J，Q，K去掉，留下A(即1)，2，3，4，5，6，7，8，9和10。隨機抽出一張牌與機率對比。 例如：假如進球機率為60%。若抽到的牌為1到6，則球投進，否則投不進。

比賽的形式

道具：棋盤，球員棋子兩色各五個，球子一個(或兩個顏色不同的球子)，及本說明書。可配撲克牌一付，或3個到5個色子。可配記分牌或紀錄卡。

球場：球場為長方形，分成11行18列的方格子，有兩個半場。每個半場包括籃筐，三秒區，兩分區和三分區。邊線及底線標記每一行和列。

比賽人數：比賽適合兩個人或兩個隊比賽。每隊一到五人或以上，可指定一個隊長或教練。教練可以要求暫停或換人。比賽可配有一個主裁判，一個副裁判。可配一個記錄員紀錄各種比賽數據，如進程，比分，技術數據等。可以使用專用的記錄卡。 團隊比賽：多人團隊的比賽，每人控制棋子的分配建議如下：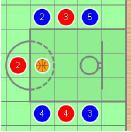

機率籃球棋

兩人隊：一人控制1，2號,一人控制3，4號，共同控制5號。

三人隊：一人控制1，2號，一人控制3，4號，一人控制5號。

四人隊：四人分別控制1，2，3，4號，共同控制5號。

五人隊：每人控制一個棋子。超過五人可以有人共同控制棋子。

比賽時隊員可用舉手的方式示意要求走棋。由裁判示意同意。先舉手者先走棋。這種玩法要求隊員之間有很好的配合及默契。可以規定不允許比賽時交談。不允許的交談可判技術犯規。可在比賽間隙或要求暫停時

商量和交代戰術。比賽規則的定製：可根據個人喜好，熟練程度等約定增加，去

除或更改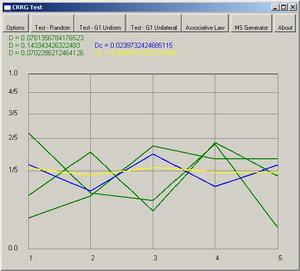

機率籃球棋

某項比賽規則。

例如：初學者只採用初級，而不採用高級的遊戲規則。

例如：更改罰球進球的機率，罰第一個球為70%，以後為80%。

例如：比賽進行期間允許棋子跑出場外(邊線及底線)一格。

例如：給某一個參賽者的進球機率增加10%。

現有的比賽規則很難包括到所有的比賽狀況。遇到特殊狀況時，可根據對真實籃球運動規則的理解和常識做出處理。 例如：裁判應該知道投球被打手犯規後在什麼情況下要判罰一個，兩個還是三個球。

沉默比賽方法：參賽者或裁判可使用真實籃球運動規則所使用的手勢參與和裁決比賽，再結合本文的其他規定，可以使比賽無需語言交流。此方法可供語言不通(如中，英文)者，及有聽或說困難或殘障的人士使用。

遊戲規則(初級)

規則概括：進攻方通過發球，傳球，運球，走動儘量爭取在投手和籃球在最靠近籃

筐的位置，並且被防守最少的情況下投兩分球或三分球。籃球離籃筐越近以及被防守越少，進球的機率越高。而防守方則儘量降低進攻方進球的機率。

機率籃球棋

比賽流程和節奏：比賽期間，兩隊輪流進攻。一個隊進攻的期間為一個進攻回合，或大回合。兩隊輪流走棋子。一個隊員走到鄰居的格子為一個子步。一個隊的所有隊員每次走一或兩個子步，合為一個隊步，或小回合。比賽期間可作各種動作(運球，傳球，投球，搶球，封蓋等，視不同級別而定)。

發球的布局：如圖4，發球隊員和籃球布置在後場靠近中線的位置，其餘球員布置在前場。如有兩個顏色不同的球子，使用顏色與進攻方相同或接近的球子。布子方法可選擇逐子或逐隊布子，明棋或盲棋布子。 逐子布子：進攻和防守方依次逐個布置棋子。發球隊員為第一個布置的棋子

。防守隊布置第二個，進攻隊布置第三個棋子。如此類推。

機率籃球棋

逐隊布子：先由進攻隊布置完其全部棋子，再由防守隊布置其全部棋子。

盲棋布子：先布置發球隊員和籃球，然後所有其它九個棋子都翻過來，使得看不見其記號，再隨意布子，最後把棋子翻過來。這種方法有很大的隨機性及娛樂性。為了快速布局，可由裁判隨意布子。如果使用沒有隱蔽功能的棋子(如圍棋子，塔形棋子等)，可用其它隱蔽方法布子。明棋布子方法布局後由進攻方首先走隊步。盲棋布子方法布局後由防守方首先走隊步。 團隊比賽的情況，隊員可以舉手示意要求布置他所控制的棋子。

格子和鄰居：每個格子有8個鄰居。上，下，左，右為近鄰。對角為遠鄰。比賽期間，兩個隊員不允許占同一個位置。球可以和進攻隊員占同一個位置。防守隊員不允許

走到球所在的位置。

機率籃球棋

控球區：一個球員的控球區包括他鄰居內的9個格子。

運球：控球隊員在進攻隊步期間可以把籃球在其控球區內任意多次移動。

傳球：球可以傳到隊友的鄰居。每次進攻隊步期間可有任意多次傳球。

搶球：如果球在進攻隊步期間走到防守隊員的控球區，或在進攻隊步結束時球在防守隊員的控球區，則球被搶。在任何情況下，防守隊員可以搶沒被進攻隊員控制的球。

投球：進攻方只有在進攻隊步期間隊員還沒有走動時才可以叫投球。如果有兩個以上的進攻隊員控制球，須指明由哪一個隊員投球。投球的結果：由機率和隨機運氣決定。投球無論進或不進都換髮球。若使用高級規則，可以搶籃板球。犯規後可罰球。

比賽結果：作為初級的隨意比賽，可約定先得一定的分數(如21分)者勝。

遊戲規則(中級)

比賽周期：每場比賽可分為一個整場，上下半場，或四節制。如需要可進入加時賽

。比賽的開始，半場制的下半場及加時賽由隨機機率模擬跳球決定首先發球進攻的球隊。四節制的每一節輪換首先進攻的球隊。

機率籃球棋

比賽的長度或計時方法可用分數或隊步數計算。每段的長度可以選定。

例如：可規定每一節為20分，加時賽每一節為10分。領先隊的分數分別到達或超過20，40，60和80分時，第一節，第二節，第三節和第四節結束。領先隊超過80分取勝。若比分為80比80則進入加時賽。如此類推。

例如：可規定整場為200個隊步，上下半場各100個隊步，四節制每節50個隊步，每次加時賽25個隊步等。

隊步的示意及計數方法：隊步的計數可使用各種計數工具。隊步走完後可叫“完 成”或通過計數工具示意輪到對方走隊步。團隊比賽的情況，隊員可用舉手的方式示意要求終止隊步。可用一個計數棋子在進攻開始時放在前場邊線的記號1上，表示正在走第一個隊步。每完成一次隊步把棋子依次移到記號2，3，4，5等。如有兩個顏色不同的球子，可用閒置的球子作為計數棋子。移動計數棋子也可作為示意終止隊步的方式。

機率籃球棋

發球：發球隊員必須在第一個隊步之內把球發到前場，並且發完球後才能移動。否則判發球違例。 換髮球：發生以下情況時換髮球：投籃之後(進球，不進，或被封蓋)，進攻方違例或犯規。

違例及犯規：進攻方違例及犯規包括發球違例，走步，球出界，回線球，球被搶，撞人犯規，3秒及24秒違例。防守方包括防守犯規，故意犯規，打手犯規。

3秒違例：若一個進攻球員在一個進攻隊步期間始終在前場三秒區內，則

判其3秒違例。

24秒違例：在一個進攻回合期間，進攻方必須在4個(可選定)進攻隊步之內投球，否則判24秒違例。或可約定如果計數棋子越過中線則違例。

碰撞子步：球員的子步是由原地走到鄰居格子。如果走到對方球員的近鄰，該子

步為碰撞。如果走到對方兩個球員的近鄰，則稱為雙碰撞。

機率籃球棋

在一個隊步期間，該隊每個球員可走一或兩個子步。第一步總是合法的。第二步在以下情況下為非法(如圖5)：1)第一及第二步均為碰撞；2)第一或第二步為雙碰撞。對進攻方非法子步規定如下：1)進攻方非法第二步判為撞人犯規。2)唯一的控球隊員試圖走第三步判為走步違例。

傳球：球移動到控球區外視作傳球。傳球分為直傳球和拋球。

直傳球：球可由起點移動到一或兩步以外的任何一個格子(如圖6)，可有橫，豎，對角，斜對角(類似中國象棋的馬步)16個方向。球傳出後沿直線路徑跳格子走下去，直到被同伴接球，被對方搶斷，出界或回線。直傳球可以即時到達。每次進攻隊步期間可有任意多次直傳球。

拋球：球可以由起點直接拋到兩步以外的任何位置，但只有在下一次進攻隊步的開始才到達終點。拋球到達終點之前不會被搶。到達終點時如果有防守隊員在鄰居，則球被搶。

機率籃球棋

“組合餘數”方法：要在N個機會均等的選項中選一個。兩個以上的人各自隨機給出一個介於1到N的數字，加起來的和除以N，得餘數，再加1給出一個介於1到N的數字。

例如：假如進球的機率為6成。比賽雙方各派一人分別給出了5和8，加起

來是13，個位數為3，加上1結果為4，在6成的機率範圍內，於是進球。

使用色子：單個色子適合做2，3，4，5，6選1。要做一般的N選1，可用多個色子做組合餘數。用3到5個色子就能給出較為均勻的機率分布。

例如：三個人搶籃板球。用4個色子分別給出點數2，5，6，3。總數為16。除以3，餘數為1，加1為2。於是第二個人搶到籃板球。

“組合餘數”最簡單而有趣的方式是象“剪刀-石頭-布”遊戲那樣猜拳用手指比劃亮出數字。如果想防止作弊和欺騙行為，可以讓中立公正的第三方(如裁判)參加。也可以利用撲克牌和色子來組合。一付撲克牌可以按花色分成4份，分別由4個人使用。也可分成紅黑，由紅藍隊使用。

“組合餘數”的數學理論可參見強方公司。

封蓋(*): 如果籃球被防守，防守隊員可選擇試圖封蓋。試圖封蓋的結果是：30%機率封蓋成功(抽到1到3)，30%機率打手犯規(抽到4到6)，40%機率既沒犯規也沒封蓋(抽到7到10)。打手犯規後無論進不進球都判罰球。封蓋成功後換髮球。

防守方撞人犯規(*)：1)如果非法子步涉及到進攻方控球隊員，則判防守犯規。控球隊員可選擇投球或重新發球。2)如果不涉及到控球隊員，裁判應根據進攻方是否處於進攻的有利位置而決定判防守犯規而重新發球，或阻止該非法子步。

對投手故意犯規(*): 如果投手被防守，防守隊員可選擇對投手故意犯規。無論進不進球都判罰球。如投手遭到防守犯規(故意犯規或打手犯規)，機率再減30%。

罰球(*)：當投手遭到防守犯規，或防守方全隊半場超過5次防守犯規，或任何球員技術犯規時，則判罰球(如圖

7)。每次罰球進球的機率均為80%。

圖7. 罰球，80%機率

籃板球(*): 投球不進時，距離籃筐兩步以內(除了站在籃筐下面)的所有球員可以搶籃板球。每個球員搶到籃板球的機率均等。可用各種機率方法決定哪一位球員搶到籃板球。

例如：在圖3的情形中，藍1號距離籃筐一步，紅3號和藍5號兩步，均可搶籃板球。紅2號距離籃筐三步，不可以搶籃板球。按照由里到外和順時針方向定，藍1號，紅3號和藍5號分別在一號，二號和三號位。在數字1到3之間抽到數字3，則三號位即藍5號搶到籃板球。搶到球的球員決定球放在那個位置。搶到球的隊先走動，並重新計時如果進攻方搶到籃板球，可立即投球或走隊步。如果防守方搶到籃板球，搶到球的球員決定重新發球或者進行快速反擊。

快速反擊(*)：防守方搶到球(斷球，籃板球等)後變成進攻方，可以決定重新發球或者進行快速反擊。

快速反擊布局(*)：快速反擊開始時，進攻和防守球員逐個輪流走動。第一個進攻球員先走任意N步，比如6步。然後其他球員走動不超過6步。第二個是防守球員走，第三個是進攻球員，如此類推，直到最後一個球員走完，快速反擊布局完畢。在這期間可以傳球。布局完畢之後進攻方開始走隊步，並開始計時。

組合餘數隨機生成

一個隨機機率數學理論:《組合餘數隨機生成之方法及原理》

資料來源：珠海強方體育文化用品有限公司

引言：人們經常需要在一組有限或無限個可供選擇的選項中隨機地選擇一個作為決策的依據。選擇方法通常可以藉助各種帶有客觀特徵的機率道具，如硬幣的正反面，多面體的擲子，撲克牌，甚至是機算計程式等。也可以不須藉助機率道具，而使用人參與的各種帶有主觀特徵的方法，如“剪刀-石頭-布”遊戲，語言，寫紙條等。所有這些方法需要解決兩個基本的問題。一是方法本身的科學性，即能模擬現實事件的隨機及機率特徵。二是方法操作上的公正性，即不能有作弊和欺騙行為，或儘可能地消除其影響。本文提出的“組合餘數隨機生成”的數學理論可以儘可能地保證隨機數字生成的科學性及公正性。

套用實例一：

甲，乙，丙三個人想在一個星期的七天之中隨機地選擇一天晚上一起上健身房鍛鍊。他們各自用自己喜歡的方式給出一個介於1到7的數字。甲決定用手指比劃給出，乙決定用撲克牌中的A，2，3，4，5，6，7給出，而丙決定把數字寫在紙上。他們同時亮出各自的數字後，把這三個數字加起來，除以7所剩的餘數加上1，所得的數即為所要的結果。舉例：甲，乙，丙分別給出3，2，6，加起來是11，11除7餘數為4，加上1為5。於是他們決定星期五晚上去鍛鍊。

套用實例二：

甲，乙兩個人要模擬籃球遊戲中進球機率為60%的一次投球的運氣。他們各自用自己喜歡的方式給出一個介於1到10的數字。甲，乙分別給出5和8，加起來是13，其個位數為3，加上1為4。結果為40%。因為是在60%的機率範圍內，於是進球。 根據本文的原理，在以上的例子中，只要任何一個人給出的數字是獨立的，即不能被其他人猜到，並且是科學而公正的，即給出任何一個數字的機率是相同的（或接近相同的），那么最終結果為任何一個數字的機率也都是相同的（或接近相同的），其他人的作弊對最終結果的科學性及公正性的影響是有限的。越多獨立的人參與選擇，其結果越為科學而公正。

“組合餘數隨機生成”數學理論的表述如下：

定義1：設G為一個服務對象，N為一個大於1的整數，G在客戶的請求下可以產生一個介於1到N的整數。則稱G為N階的數字生成器。如果生成的整數是隨機的，則稱其為隨機的。如果隨機生成的整數有確定的機率分布，則稱其為機率確定的。如果其機率分布是均勻的，則稱其為機率均勻的。

定義2：兩個數字生成器如果其生成的數字之間沒有任何數學關係，即不能通過某種確定的方法根據一個數字去確定另一個數字的特徵。則稱該兩個數字生成器為數學不相關。

定義3：設G為一個N階的(N>1)機率確定的數字生成器，其生成介於1到N的數字i的機率為Pi。定義G的機率均方差為：

D=Σ(i=1toN)[Pi–1/N]**2

它是機率分布偏離均勻分布及機率均勻度的一個度量。D越小，偏離均勻分布越小，均勻度越高。

組合餘數生成之方法：設{Gi}(i=1,…,M,M>1)為一組N階的(N>1)數字生成器，G為一個由該組生成器組合成的一個組合生成器。G生成的整數是該組所有生成器生成的整數之和除以N所得的餘數加上1，則G也為一個N階的數字生成器，稱為M重的組合餘數生成器，表示為G=C(G1,G2,…,GM)。

組合餘數生成之交換律及結合律：設G1，G2及G3為三個N階的(N>1)數字生成器，則

C(G1,G2)=C(G2,G1)

C(C(G1,G2),G3)=C(G1,C(G2,G3))

組合餘數隨機生成之原理：設{Gi}(i=1,…,M,M>1)為一組N階的(N>1)數字生成器，G為其組合餘數生成器。如果其中一個生成器Gk(k介於1到M)與該組其他生成器均為數學不相關。則以下原理成立：

隨機原理：

如果Gk為隨機的，則G也為隨機的。 機率均勻原理：如果Gk為機率均勻的，則G也為機率均勻的。

機率均方差之極限原理：設G為一個N階的(N>1)機率確定的數字生成器，D為其機率均方差，其極限為:

0≤D≤1–1/N

如果機率分布是均勻的，則D=0。如果生成某一個數字的機率為1而其餘為0，則D=1–1/N。

組合餘數隨機生成之機率均方差之原理：設G1及G2為兩個N階的(N>1)數學互不相關的機率確定的數字生成器，G為其組合餘數生成器，D1，D2和D分別為它們的機率均方差，則以下原理成立：

機率均方差之極限原理：D≤N*D1*D2

近均勻生成器之組合均勻化原理：如果G1為一個近均勻生成器，即存在一個d1≥0使其所有機率均差|Pi–1/N|≤d1/N,則D1≤d1**2/N,因而D≤d1**2*D2。如果d1<<1，則D<< P>

組合餘數隨機生成之機率均勻化原理：設{Gi}(i=1,…,M,M>1)為一組N階的(N>1)數學互不相關的機率確定的數字生成器，G為其組合餘數生成器，D為G的機率均方差。設{G′i}(i=1,…,M′,M′>1)為{Gi}(i=1,…,M,M>1)的一個子集，即{G′i}∈{Gi}，G′為其組合餘數生成器，D′為G′的機率均方差，則：

D≤D′

因而對於{Gi}中的任何一個生成器Gi及其機率均方差Di有：

D≤Di(i=1,…,M)

數學證明：

從略。 註：本理論結合著名的“主控-從屬”(Master-Slave)及“組合”(Composite)軟體設計模式在遊戲軟體中的套用被用作中國科學院研究生院計算與通信工程學院(原軟體學院)軟體工程碩士2006年春季《軟體體系結構》課程的教學案例。此前，其中的“機率均勻化原理”原為一個未被普遍證明的數學猜想。該課程的部分學員對該數學理論表現出了極大的興趣。其中陳更新同學所提供的思路使得這一猜想的普遍性在數學上得以證明。在此對參與討論和交流的所有學員表示衷心的感謝。

計算驗證：

利用電腦程式隨機產生的機率分布，結合一些人為選擇的特殊的機率分布，再利用電腦程式進行生成器組合及分析，可以對本理論的原理進行驗證，並且直觀了解組合生成器的特性(如圖所示)。到目前為止驗證的結果一直支持本理論而沒有發現反例。