樹形檢索是資料庫的一種索引方式。樹形索引的建立，使得對數據的查找變得便利了許多，而不需要從頭至尾的遍歷所有數據。
建立索引之後，資料庫將會自行維護類似的樹形索引，便於查詢。但也正是樹形索引的維護，使得對數據的增加和刪除操作變得耗時，同樣也增加了數據所占用的存儲資源。
無論是專用的資料庫，還是作業系統的檔案系統，都會利用樹形索引來管理數據的存儲和查詢。
基本介紹
- 中文名：樹形檢索
- 外文名：binary-tree searching
- 類型：數據索引方式
- 作用：方便查詢數據，無需遍歷數據
- 用處：專用資料庫、作業系統檔案系統
檢索介紹,種類,具體操作,
檢索介紹
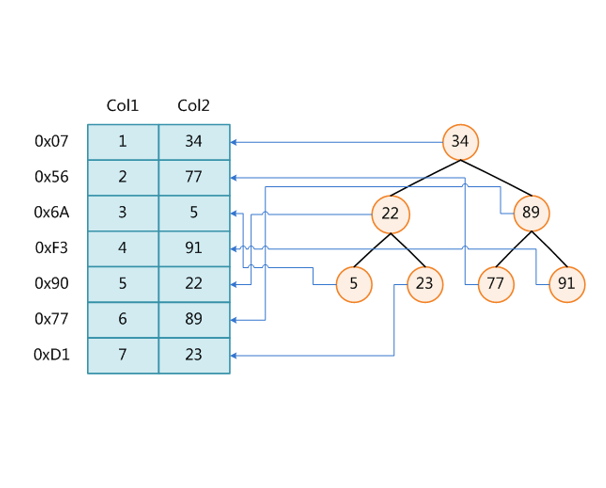
如圖1所示給出的是資料庫中常用索引的示意圖。左半邊圖所表示的是完整的數據表，右半邊是對表中Col2列數據建立的樹形索引。樹形索引的建立，使得對Col2數據的查找變得便利了許多，而不需要從頭至尾的遍歷Col2中的所有數據。通過上述這個例子，相信大家應該也理解了，為什麼要對資料庫中經常查找的數據建立索引。建立索引之後，資料庫將會自行維護類似圖右側的樹形索引，便於查詢。但也正是樹形索引的維護，使得對數據的增加和刪除操作變得耗時，同樣也增加了數據所占用的存儲資源。
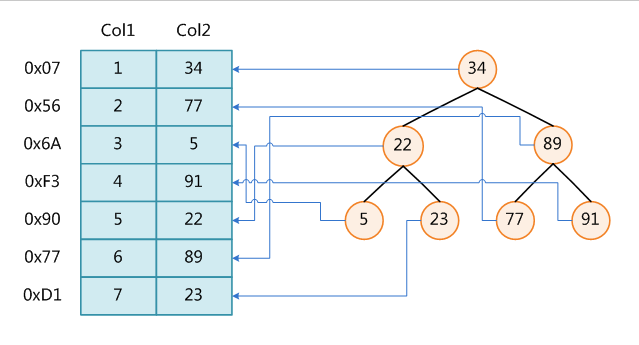
圖1
種類
2-3樹
2-3樹不是一種二叉樹，但它的形式符合下面的定義：
（1）一個節點包含一個或兩個關鍵碼；（2）每個內部節點有兩個子節點（包含一個關鍵碼）或者三個子節點（包含兩個關鍵碼），因此得名為2-3樹；（3）所有葉節點都在樹形結構的同一層，因此輸的高度總是平衡的，下面是一顆典型的2-3樹。
圖2
對於每個節點，其左子樹中所有節點的值都小於第一個關鍵碼的值，而中間子樹的所有節點值都大於或等於第一個關鍵碼的值；如果右子樹存在的話，那中間子樹所有節點的值還需小於第二個關鍵碼的值，而其右子樹的所有節點值都大於或等於第二個關鍵碼的值。
B樹
B樹是一種很常用的索引樹，說是到了1972年，B樹幾乎替代了除散列方法之外的所有大型檔案訪問方法，一個m階（度數為m）B樹定義為一下特點：
（1）除了葉節點，其他節點至少有兩個子節點；（2）除了根節點，每個內部節點有[m/2]到m個子節點；（3）所有葉節點都在樹結構的同一層，同為樹高度平衡。如圖3所示給出一顆典型的B樹示意圖。
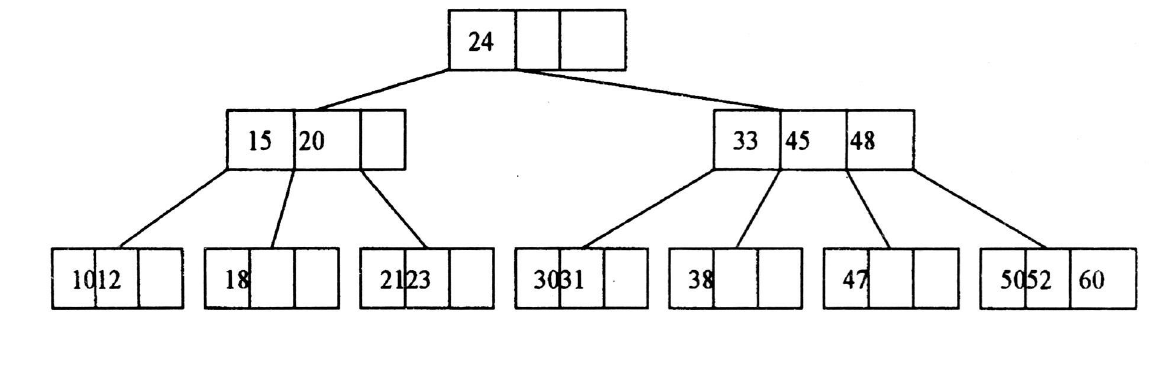
圖3
B樹是2-3樹的一種推廣，B樹節點的實現一般允許其具有上百個甚至更多的子節點。B樹的深度將比2-3樹來的小，所以將由更高的查找效率。
B+樹
B+樹是一種B樹的變體，理論上來說，B樹可以廣泛地用於實現基於側畔的大型系統，但卻從來沒有實現過，最普遍使用的是B+樹。給出B+樹的定義如下：
（1）書中每個非葉節點最多有m個子節點；（2）根節點至少有兩個子樹，除根外，所有的非葉節點至少有[m/2]個子節點，有n個子節點的非葉節點有n-1個關鍵值域；（3）所有葉子節點處於同一層上，包含了全部關鍵值以及指向相應數據對象存放地址的指針，且葉節點本身按鍵值從小到大順序連結；（4）所有的非葉節點可以看作為索引部分，節點中關鍵值與指向子樹的指針構成了對樹的索引項。如圖4所示給出B+樹的示意圖。
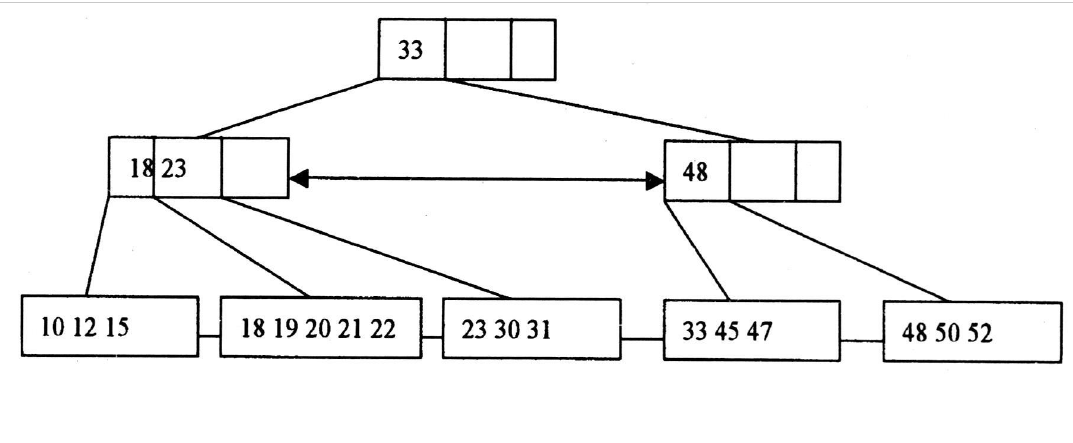
圖4
B+樹與B樹最顯著的區別在於：B+樹只在葉節點存儲記錄，內部節點存儲關鍵碼值，這些關鍵碼值只是用於引導索引檢索位符，以為這B+樹的內部節點和葉節點在結構上有著顯著的區別。內部節點存儲關鍵碼引導索引，每個關鍵碼與一個指向子節點的指針相關聯，而葉節點存儲實際記錄。
具體操作
插入（INSERT）操作：
插入一個元素時，首先判斷在B樹中是否存在，如果不存在，即在葉節點處結束，然後在葉節點中插入該新的元素，注意：如果子節點空間足夠，這裡需要向右移動該葉節點中大於新插入關鍵字的元素；如果空間已滿，則將該節點進行“分裂”，將一半數量的關鍵字元素分裂到新的其相鄰右節點中，中間關鍵字元素上移到父節點中（如果父節點空間已滿，同樣執行“分裂”操作）。如果在根節點中插入新元素，使得根節點需要進行“分裂”，這樣原來的根節點中的中間關鍵元素向上移動成為新的根節點，使輸的高度增加一層。
刪除（DELETE）操作
雖然刪除是插入操作的相反動作，但是在刪除節點時，需要考慮較多的因素。首先查找B樹中需要刪除的元素，如果該元素在B樹中存在，則將該元素再起節點中進行刪除，如果刪除該元素後，首先判斷該元素是否有左右子節點。如果有，則上移自己點中的某相近元素到父節點中，然後考察移動之後的情況；如果沒有，直接刪除，再考察。進行再次考察時，如果某節點中元素數目不滿足最低要求，則需要看其某相鄰兄弟節點是否豐滿。如果豐滿，則向父節點借一個元素來滿足條件；如果其相鄰兄弟都剛脫貧，即借了之後節點數目不夠最低標準，則該節點與其相鄰的某一兄弟節點進行一次合併，以此來滿足條件。
