模2運算是一種二進制算法,CRC校驗技術中的核心部分。與四則運算相同,模2運算也包括模2加、模2減、模2乘、模2除四種二進制運算。而且,模2運算也使用與四則運算相同的運算符,即“+”表示模2加,“-”表示模2減,“×”或“·”表示模2乘,“÷”或“/”表示模2除。與四則運算不同的是模2運算不考慮進位和借位,即模2加法是不帶進位的二進制加法運算,模2減法是不帶借位的二進制減法運算。這樣,兩個二進制位相運算時,這兩個位的值就能確定運算結果,不受前一次運算的影響,也不對下一次造成影響。
基本介紹
- 中文名:模2運算
- 外文名:mod 2
- 釋義:一種二進制算法
- 所屬學科:數學
模二加法,模二減法(等價於按位異或),模二乘法,模二除法,
模二加法
一種二進制的運算,等同於“異或”運算。 通常用於計算機和電子領域。規則是兩個序列按位相加模二,即兩個序列中對應位,相加,不進位,相同為0,不同為1。
1+1=0+0=0
1+0=0+1=1
0 1 0 1
+ 0 0 1 1
──────
0 1 1 0
0 1 1 0
模二減法(等價於按位異或)
0-0=0
0-1=1
1-0=1
1-1=0
例如0110-0011=0101,列豎式計算:
0 1 1 0
- 0 0 1 1
──────
0 1 0 1
0 1 1 0
- 0 0 1 1
──────
0 1 0 1
模二乘法
0×0=0
0×1=0
1×0=0
1×1=1
多位二進制模2乘法類似於普通意義上的多位二進制乘法,不同之處在於後者累加中間結果(或稱部分積)時採用帶進位的加法,而模2乘法對中間結果的處理方式採用的是模2加法。例如1011×101=100111,列豎式計算:
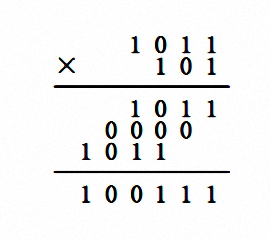 模二乘法示例
模二乘法示例模二除法
1111000除以1101


