基本介紹
- 中文名:模糊測度論
- 所屬學科:數學(模糊數學)
- 簡介:處理廣義模糊性的理論
基本介紹,基本概念,模糊測度,λ模糊測度,
基本介紹
所謂積分,無論是黎曼積分還是勒貝格積分都不外乎是被積函式和測度函式的一種內積,不同的只是以不同的測度為基礎。因此研究模糊積分要從研究模糊測度開始。
模糊測度有多種解釋,M.Sugeno對模糊測度做了這樣的解釋:設有某個元素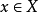 ,我們猜想x可能屬於A的某個元素A(即A∈A,且
,我們猜想x可能屬於A的某個元素A(即A∈A,且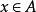 )。這種猜想是不確定的,是模糊的。
)。這種猜想是不確定的,是模糊的。
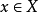
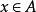
一個確定的點對於一個模糊集合的隸屬程度,是經典集合論中點對集合屬於關係的一種推廣。模糊測度是普通屬於關係的另一種推廣,即一個尚未確定的點(信息不充分條件下)對於經典集合的屬於關係。可能性測度在實際問題中是最常見的模糊測度,如海底礦藏測量。
為了研究模糊測度的結構和模糊積分的計算,日本著名學者M.Sugeno於1974年提出λ測度的概念,其核心思想是將機率測度的可加性放寬。
基本概念
模糊測度
設(X,σ)是可測空間,如果映射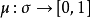 滿足:
滿足:
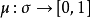
1.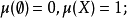
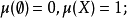
2.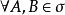 ,若
,若 ,有
,有 ;
;
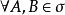


3.若 ,且
,且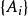 單調,有
單調,有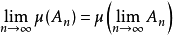 ;
;

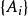
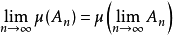
則稱μ為模糊測度,(X,μ)稱為模糊測度空間。
模糊測度是由菅野道夫(M.Sugeno)於1974年提出的,它的研究是與具有主觀性複雜系統的評價問題緊密相關的。目前,也有人將建立在模糊子集族構成的σ代數上的測度稱為模糊測度。設Σ是X的模糊子集族,稱Σ為由模糊子集構成的σ代數,如果Σ滿足條件:
1.任何X的經典子集屬於Σ。
2.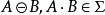 ,此處
,此處
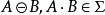

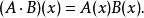
3.若 ,有
,有 ,此處
,此處



而從Σ到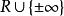 滿足條件:
滿足條件:
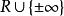
1.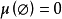 ;
;
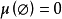
2.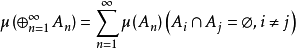
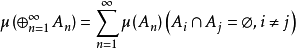
的映射稱為模糊測度,這與第一種定義的模糊測度是根本不同的。
λ模糊測度
λ模糊測度(λ-fuzzy measure)是一種模糊測度,它是帶參數λ的一種重要的模糊測度。設(X,σ)是可測空間,如果映射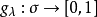 滿足以下條件:
滿足以下條件:
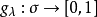
1.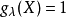 ;
;
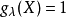
2.對於σ中不相交的集合A與B,
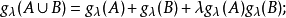
3.對σ中的單調集合列 ,有
,有

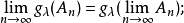
設 ,模糊分布函式H(x)滿足
,模糊分布函式H(x)滿足 ,記
,記


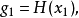
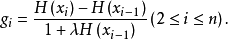
對任何A⊂X,定義