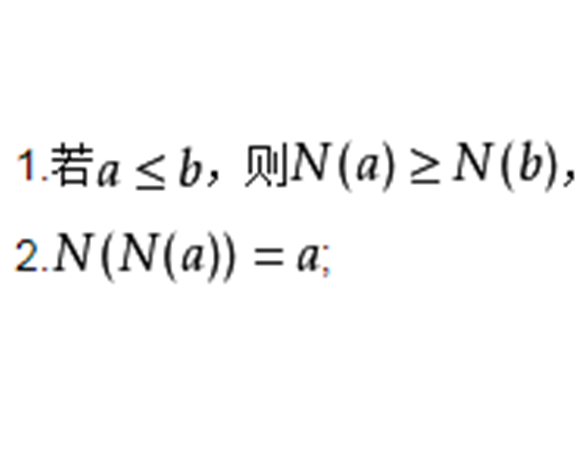模糊格

模糊格(fuzzy lattice)是一類特殊的完全分配格，由於這種格與模糊數學的結構有緊密的聯繫，所以人們稱其為模糊格。模糊格是對傳統格理論的拓展，它考慮了格中兩個元素之間的關係，為定量描述模糊格中兩個元素之間的包含關係，V.Petridis還提出了包容性測度的概念。

基本介紹

• 中文名：模糊格
• 外文名：fuzzy lattice
• 所屬學科：數學（模糊數學）
• 簡介：一類特殊的完全分配格
• 提出者：Petridis V

基本介紹

設L是格，a∈L稱為並既約元，若對L的任意元x和y，當a=x∨y時，有a=x或a=y，L的非零並既約元稱為分子，由於完全分配格具有充分多的分子，因此，常稱完全分配格為分子格。若L是分子格且帶有逆序對合對應，即存在映射滿足：

1.若，則，

2.;

則稱L是模糊格。若：

1.f是保並映射;

2.f^-1是保逆合映射，即對，有

則從模糊格L₁到模糊格L₂的映射f稱為序同態。

相關分析

在完備格理論的基礎上，Petridis V提出了一個新的格學習框架——模糊格(Fuzzy lattice)，其定義為：

假設L為一個格，為一個分布，是一個模糊隸屬度函式，且滿足若且唯若x≤y時，，則稱為一個模糊格，其中實值函式可以解釋為x包含於y的程度。

模糊格是對傳統格理論的拓展，它考慮了格中兩個元素之間的關係，為定量描述模糊格中兩個元素之間的包含關係，V.Petridis提出了包容性測度的概念，其定義為：

假設L為一個完備格，其最小元素與最大元素分別為O和I，則包容性測度定義為，且滿足以下條件：

(1)；

(2)

(3)。

由條件(2)和(3)可以很容易地得出以下結果：

進一步可以得出。因此，表示了格關係x≤u的真實程度，即x包容於u的程度。

為了進一步量化包容性測度，定義實值函式，它主要滿足以下幾個條件：

(1)為格L中的最小元素；

(2)

(3)

函式h在格L上不一定存在，假如函式h存在，則函式是一個定義在格L上的包容性測度。可以看出

因此，定義了一個模糊格。我們簡單地設函式：。

假設L為Ⅳ個格的笛卡兒積：，其偏序關係定義為

則在L上的函式h可定義為

可以證明滿足前述的3個條件。