模擬植物生長算法

模擬植物生長算法(PGSA)作為一種智慧型最佳化算法,是以植物向光性的機率生長動力機制為啟發式準則的,在解決斯坦納最小樹問題、物流設 施選址問題、整數規劃問題以及各類工程最佳化問 題的套用當中,該算法表現出了較強的全局搜尋能力,具有計算精度高,穩定性好和套用性強的特點.

基本介紹

• 中文名：模擬植物生長算法
• 外文名：PGSA

基本信息

模擬植物生長算法(PGSA)是在2005年提出的一種以植物向光性機理為啟發式準則的智慧型最佳化算法.該算法是將植物系統演繹模式(L一系統)和植物系統機率生長模式(向光性)向最佳化領域進行映射和變異的典型套用.PGSA提出3年來,在整數規劃、組合最佳化以及工程技術領域逐漸顯示出其突出的穩定性、精確性和全局搜尋能力,因而具有良好的套用和推廣前景.

所謂PGSA,就是將最佳化問題的解空間當作植物的生長環境,將最優解當作光源,模擬真實植 物的向光性機理(形態素濃度理論),建立枝葉在不同光線強度環境下的快速生長的生長演繹方式 (L-系統).PGSA的研究重點是建立以生長規則為基礎的植物系統演繹方式和以植物向光性理論為基礎的機率生長模型,兩者結合所形成的最佳化模式,就是實現人工植物在最佳化問題解空間中從初始狀態到完整形式的終態(沒有新的樹枝生長)的過程.

植物生長的演繹模式

植物可看作由大量枝、節組成的系統,模擬植物的生長演繹方式是A.Lindenmayer在20世紀 60年代末把喬姆斯基的生成轉換語法引入生物學,以簡單的重寫規則和分枝規則為基礎,建立了關於植物的描述、分析和發育模擬的形式語法,稱為L-系統.對植物生長作形式化描述,可以根據以下幾點進行:1)破土而出的莖桿在一些叫做節 的部位長出新枝;2)大多數新枝上又長出更新的枝,這種分枝行為反覆進行;3)不同的枝彼此有相似性,整個植物有自相似結構.用L-系統描述生長的基本概念如圖1所示.

L-系統分形成長過程

20世紀80年代,P.Prusinkiewicz等人把L-系統與計算機圖形學、分形學結合起來,完善了植物生長的分枝模型.在所規定的生長規則的反覆重寫下,可作出如圖2所示的分形生長樹圖(取自普魯森科維奇專著).

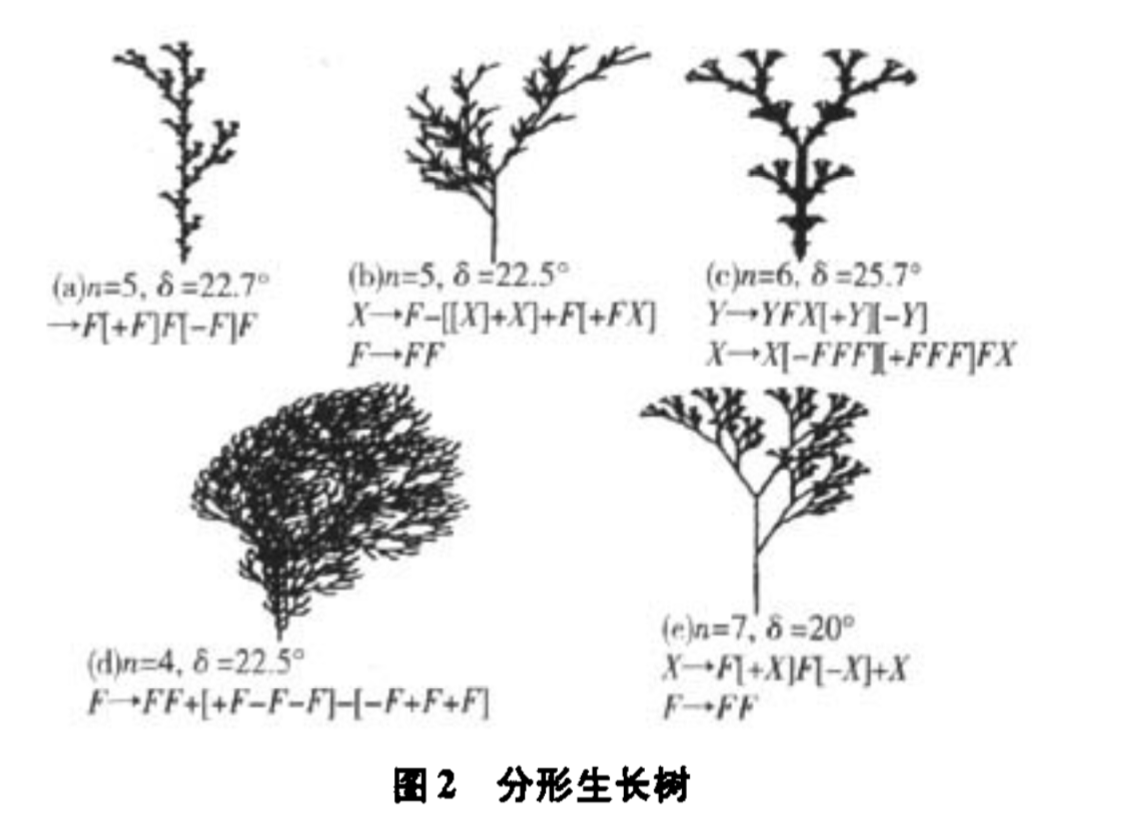圖2 分形生長樹

PGSA以L-系統作為人工植物的生長演繹方式的源模式,生長點即植物生長細胞,是模擬植物系統每一次生長的位置點.植物生長過程是在生長點按2n(廳為變數的維數)個方向生長並產生新枝,分枝長度在整數規劃情況下設定為1(非整數規劃情況下可根據精度要求選取).

按照L-系統完成的人工植物結構,僅解決了模擬植物生長的演繹問題,其關鍵問題還沒有解決,即在眾多生長點中,每一次到底確定其中哪一個進行新的生長,怎么保證樹枝向最優解方向生長,其核心問題就是植物向光性特點的算法實現問題.

植物向光性的機率生長模式

植物向光性涉及生物學理論中的形態發生模型,該模型是用複雜動力系統為生物生長建模的著名例子,模式的形成被理解為複雜過程,其中一個細胞發生分化,產生出新的明確定義的空間結構.形態發生的最初的動力學模型是拉什夫斯基、 圖林等人提出來的.他們關於植物生長形態發生 (“葉序”)模型如圖3所示,葡萄莖梗發出一個枝芽的某一時刻,它出現在對於3個枝芽對稱旋轉 的方向(PGSA將旋轉方向確定為90度).在生長中的莖梗的頂部,生長出來一個芽,包含著未分化的細胞.葉序問題涉及作為葉芽細胞、分枝細胞和其他導致葉芽和分枝的分化細胞的生長模式的形成.一個細胞被看作是一個流體袋,其中有均勻的化學組分,其中的一種化學組分是生長激素,叫做形態素.這種形態素的濃度名是此模型的觀察參量,隨著參量在0和1之間變動,模型的狀態空間是一條線段(圖4).這種形態素的濃度決定細的生長函式是否開始起作用,即細胞分裂,枝芽開始出現.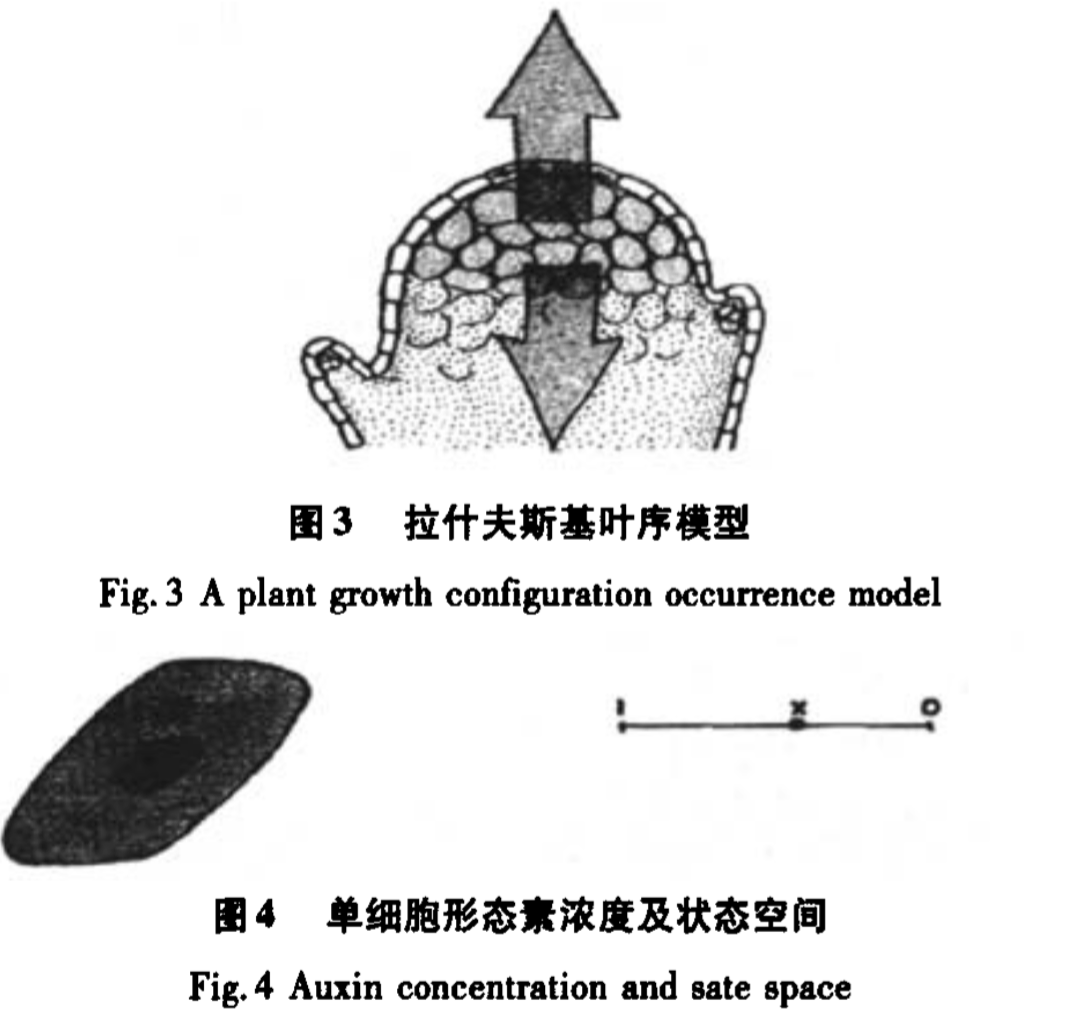

圖3 圖4

新的生長點(細胞)產生後,形態素濃度將根據新系統所在環境的改變,重新進行分配.在多細胞系統中,如果把任意一個細胞形態素濃度記為 Pi(i=1,2,⋯,n),則多細胞封閉系統形態素狀態空間用見圖5,且濃度和是恆定的(設定為1). 生物學實驗已經證明,決定植物細胞分裂和枝芽生長的生長素信息(形態素濃度)並非是預先一個個賦予給細胞的,而是細胞系統從其環境中接 受到了它的位置信息,依據這種信息,植物表現出明顯的向光性特點.模擬這一過程,設有n個初始生長點Si=(S1,S2,⋯,Sn),每一個生長點的形態素濃度為Pi=(P1,P2,⋯,Pn),當目標函式實現最小化時,計算各生長點形態素濃度值為式(1)

其中以f(·)為目標函式值.式(1)中,各生長點形態素濃度是由各點的相對位置以及該位置的環境信息(目標函式值)所確定,這與真實植物細胞的形態素濃度生成機理相一致.因此,n個生長點均對應n個形態素濃度值,每次產生新枝,該濃度值都將發生變化.

由式(1)可知式2

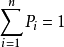
在確定了形態素濃度之後,就可以建立植物的向光性機制,即形態素濃度較高的生長點(細胞),將具有較大的優先生長機會,其算法可描述為:設共有n個生長點(S1,S2,⋯,Sn),按照公式 (1)分別計算其形態素濃度值為(P1,P2,⋯,Pn),式(2)已經得到Pl+P2+⋯+Pn=1,因此其機率空間如圖5所示.

圖5 形態素濃度機率空間

計算機系統不斷產生隨機數,這些隨機數就象不斷向區間[0,1]上投擲的小球,小球落在P1, P2,⋯,Pn的某一個機率空間內,所對應的生長點就得到優先生長的權利.這個過程反覆進行,模擬植物的樹枝按照L-系統生長模型在解空間內快速蔓延,直至沒有新枝的產生為止,這就是 PGSA,其疊代過程詳見文獻.

PGSA的套用

一種新算法的提出,必須具有解決現實問題的能力,否則無論理論體系如何完整,也不會被廣泛套用和認可,也就缺乏進一步發展的可能性.下文以PGSA解決斯坦納最小樹問題切入點,同時 對目前PGSA在不同領域的套用情況做一個簡要 的總結.

PGSA在斯坦納最小樹問題中的套用

斯坦納最小樹(SMT)問題最早可追溯到法國數學家費馬(P.de Fermat)1634年所提出的費馬問題“.目前該問題是組合最佳化中著名的NP難題,是指連線給定點(Girven point,或稱所與點)的最小樹長問題.若x為平面上給定n個點的點集,設G是由某些邊構成的圖形,邊的端點叫做G的頂點.若G的頂點集包含x中所有點,則稱G為x的生成樹,當樹的總長度最短時,則稱之為最小生成樹(MST),其長度記作(X).如果除了n中的點外,還可以用n點以外的點(斯坦納點)作為樹的結點,則這樣的樹即稱為斯坦納最小樹(SMT),其長度記作(X).

模擬植物生長算法(PGSA)在解決SMT問題上以斯坦納比(X)/(X)為標準與文獻[8]中螞蟻算法(AA)、模擬退火算法(SA)進行了精度比較,實驗採用國際上公布的測試資料庫STEINLIB中的問題實例,算法用Matlab編程實現,在Windows XP平台上運行通過,試驗中計算機為Celeron(R) CPU 3.06GHz,1.00GB記憶體. PGSA在STEINLIB中的每個測試實例分別進行15次計算,其中最好結果與最差結果之間誤差值不超過0.017%,表現出了算法突出的計算穩定性。

算法在各學科領域中的套用

除了解決組合最佳化問題,PGSA目前在整數規劃和工程技術領域已逐步被許多國內外學者套用.

K.Guney、A.Durmus和S.Basbug在文獻[9]中將模擬植物生長算法(PGSA)用於電磁學中的干擾幅度控制領域,分別於MTACO、BA、BFA三種智慧型算法比較,PGSA均得到了更優的結果,且收斂性和計算速度明顯優於其他算法.他們的套用結論為:“As an optimization algorithm, the PGSA will most likely be an increasingly attractive alternative, in the electromagnetics and antennas community ,to other optimization algorithms.’’

R.Srinivasa Rao、S.V.L.Narasimham在文獻[10]中套用PGSA來解決雷達分配系統中電容最佳化配置的問題.他們的套用結論為:“The advantages with the Plant Growth Simulation algorithm(PGSA)is that it treats the objective function and constraints separately ,which averts the trouble to determine the barrier factors and makes the increase/decrease of constraints convenient ,and that it does not need any external parameters such as crossover rate,mutation rate, etc.It adopts a guiding search direction that changes dynamically as the change of the objective function.’’

在國內,上海交通大學、大連理工大學、哈爾濱工業大學、鄭州大學、華北電力大學等高校的學者也分別在不同領域對PGSA進行了套用研究.

文獻對模擬植物生長算法進行了一些改進,採用植物頂點變速度生長特點來減少搜尋時間,利用植物生長期前期縱向型生長特性來減少搜尋空間,因此能夠在更少的時間內得到更優解.通過對不同類型的非線性整數規划算例求解, 表明該算法是很有效的.

文獻中運用PGSA與其他最佳化算法進行了比較研究,結果表明PGSA給出的最優網路是現有文獻當中最好的方案,明顯優於遺傳算法和粒子群算法.

文獻的計算結果表明PGSA優於遺傳算法和協同進化算法.

文獻中的分析計算表明PGSA與遺傳算法、Tabu搜尋算法相比，具有更高的精度和更加快速的全局尋優能力。

文獻中建立了動態無功最佳化的模擬植物生長算法,算法對負荷按實際形狀而不是按設備動作次數限制進行分段,更加準確地描述了負荷的實際狀況,所得到的無功補償最佳化投切方案能更好的滿足電網實際運行的需要。

文獻中對PGSA做過一個總結:“理論分析及算例結果表明,與遺傳算法為代表的現代啟發式算法相比,模擬植物生長算法具有以下優點:1模擬植物生長算法將目標函式和約束條件分開處理,且無需編碼和解碼,避免了構造新的計算用目標函式,也不存在懲罰係數、交叉率、變異率選取等問題，解的穩定性好；2.模擬植物算法具有一個由形態素濃度決定的方向性和隨機性平衡比較理想的搜尋機制,能以較快的速度尋找到全局最優解.”

文獻中,通過對IEEE 30節點系統採用 模擬植物生長算法、標準遺傳算法和粒子群最佳化 算法比較,模擬植物生長算法得到的最佳化方案網損最小,同時有更強的收斂穩定性.

文獻將PGSA用於設施選址問題,比較研究結果表明PGSA優於遺傳算法.

PGSA的研究領域還包括:我國著名水處理專家,哈爾濱工業大學李圭白院士等將PGSA推廣套用於雙級決策的排污收費模型,改進了傳統 的最優Pigovian定價法的諸多問題;西南石油大學的張偉等人將PGSA套用於三維地震勘探的採集、處理等地震勘探最佳化問題;此外,羅偉強、焦彥軍、楊麗徙、王鍇、趙穎等人套用模擬植物生長算法在各自的領域進行了大量的套用研究。