標籤傳播(LPA)算法是最早的基於標籤的一種算法,是所有基於標籤的算法的基礎。標籤傳播算法最大的特色是簡單、高效,缺點是每次疊代結果不穩定,準確率不高。
在標籤傳播算法基礎上改進的標籤算法有COPRA、SLPA等。
基本介紹
- 中文名:標籤傳播算法
- 外文名:LPA
算法簡介
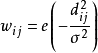


標籤傳播(LPA)算法是最早的基於標籤的一種算法,是所有基於標籤的算法的基礎。標籤傳播算法最大的特色是簡單、高效,缺點是每次疊代結果不穩定,準確率不高。
在標籤傳播算法基礎上改進的標籤算法有COPRA、SLPA等。
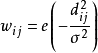

標籤傳播(LPA)算法是最早的基於標籤的一種算法,是所有基於標籤的算法的基礎。標籤傳播算法最大的特色是簡單、高效,缺點是每次疊代結果不穩定,準確率不高。在標籤...
LPA算法的基本思想是為網路中所有的節點賦予不同的標籤,設計一個傳播規則,標籤根據這個規則在網路上疊代傳播,直到所有節點的標籤傳播達到穩定,最後將具有相同標籤的...
SLPA算法是一種社區監測算法,它是對LPA算法(標籤傳播算法)的拓展。...... SLPA算法是一種社區監測算法,它是對LPA算法(標籤傳播算法)的拓展。中文名 SLPA算法 外...
基於最佳化標籤傳播算法的社區發現方法研究, 情報學報, 2014, 33(5):538-548. 章成志. 基於多層術語度的一體化術語抽取研究, 情報學報, 2011, 30 (3): 275-...
》在第2、3、4章介紹了圖的基礎知識、GraphX基礎知識、GraphX內置的圖算法。...7.4.2 半監督學習標籤傳播算法 1757.5 小結 180第3部分 更多內容...
8.4 內置的圖算法 2798.4.1 PageRank 2798.4.2 計算三角形數 2828.4.3 計算連通分量 2848.4.4 標籤傳播算法 2858.4.5 SVD++ 2868.5 GraphX實現經典圖算法...
智慧型算法105搜尋引擎的查詢意圖識別105社交網路:數據科學家眼中的金礦107標籤傳播算法在微博用戶興趣圖譜的套用109基於大規模語料的新詞發現算法112...
