基本介紹
- 中文名:標準回歸係數
- 外文名:Standard regression coefficient
- 學科:數學、統計學
- 特點:可能因時因地而變化
前提
定義
公式
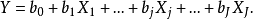

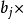
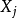

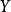

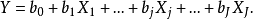

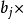
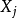

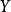
標準回歸係數,是指消除了因變數和自變數所取單位的影響之後的回歸係數,其絕對值的大小直接反映了自變數對因變數的影響程度。標準化回歸係數的比較結果只是適用於某一...
用最小二乘法求回歸直線方程中的a,b有下面的公式:回歸方程的寫法:spss數據表中有非標準係數一欄,這其實就是回歸方程的係數。對應的變數就是和係數相乘。如果有...
決定係數(coefficient of determination),有的教材上翻譯為判定係數,也稱為擬合優...但從本質上說決定係數和回歸係數沒有關係,就像標準差和標準誤差在本質上沒有...
嶺回歸通過給回歸估計值添加一個偏差值,來降低標準誤差。線上性等式中,預測誤差...R2又稱為方程的確定性係數(coefficient of determination),表示方程中變數X對Y的...
確定亦稱測定係數、決定係數、可決指數。與復相關係數類似的,表示一個隨機變數與多個隨機變數關係的數字特徵,用來反映回歸模式說明因變數變化可靠程度的一個統計指標,...
其中ρam為證券 a 與市場的相關係數;σa為證券 a 的標準差;σm為市場的標準差。貝塔係數利用回歸的方法計算: 貝塔係數等於1即證券的價格與市場一同變動。...
社會經濟現象的變化往往受到多個因素的影響,因此,一般要進行多元回歸分析,我們把...這時的回歸方程稱為標準回歸方程,回歸係數稱為標準回歸係數,表示如下:...
判定係數(coefficient of determination),也叫可決係數或決定係數,是指線上性回歸中,回歸平方和與總離差平方和之比值,其數值等於相關係數的平方。它是對估計的回歸...
1.篩選標準與原則。對於自變數各種不同組合建立的回歸模型,使用全局擇優法選擇“最優”的回歸模型。(1) 殘差平方和縮小與決定係數增大。如果引人一個自變數後模型...
回歸方程的精度與簡潔性的標準往往不可能同時得到最大化的滿足。在回歸方程精度的測量指標中,最常用的指標是復判定係數。復判定係數的一個重要性質是,它是出現在...
因徑係數是一種回歸方程的回歸係數。在因徑分析中,每一局內變數均可用一線性標準回歸方程表示,方程中標準化的回歸係數稱因徑係數。表示因果效應的解釋力。因徑...
這種函式是一個或多個稱為回歸係數的模型參數的線性組合。只有一個自變數的情況...在決定一個最佳擬合的不同標準之中,最小二乘法是非常優越的。這種估計可以表示...
標準差係數,又稱為均方差係數,離散係數。它是從相對角度觀察的差異和離散程度,在比較相關事物的差異程度時較之直接比較標準差要好些。...
在統計學中,線性回歸是利用稱為線性回歸方程的最小二乘函式對一個或多個自變數和因變數之間關係進行建模的一種回歸分析。這種函式是一個或多個稱為回歸係數的模型...
擬合優度(Goodness of Fit)是指回歸直線對觀測值的擬合程度。度量擬合優度的統計量是可決係數(亦稱確定係數)R²。R²最大值為1。R²的值越接近1,說明...
