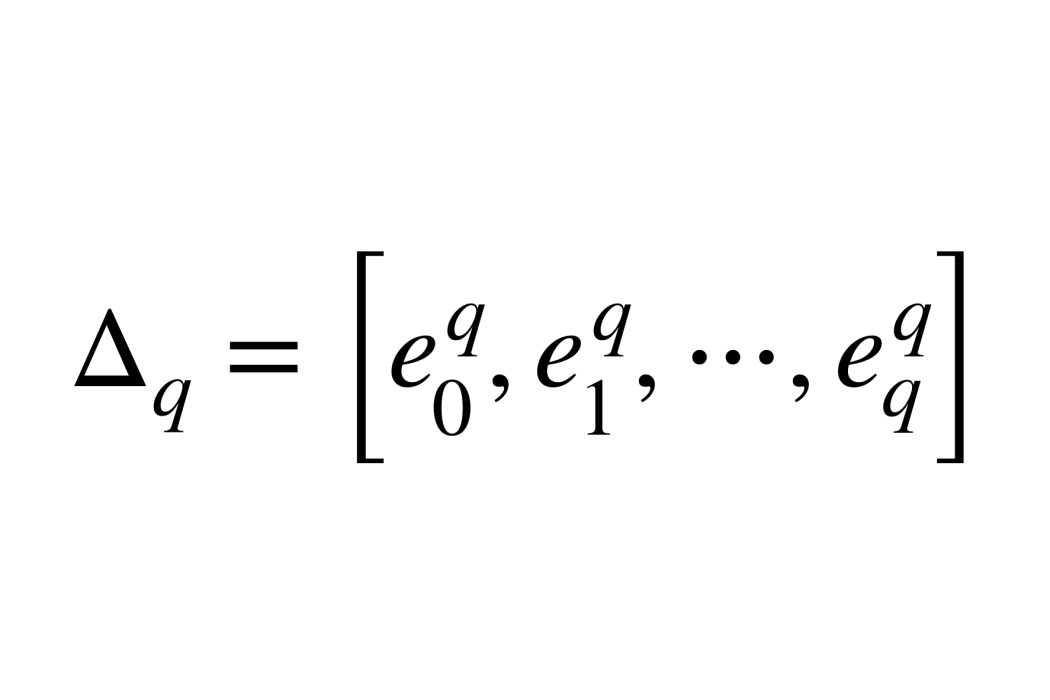標準單形是一類特殊的單形，它在研究復形性質及奇異同調理論時都要用到。
基本介紹
- 中文名：標準單形
- 外文名：standard simplex
- 適用範圍：數理科學
- 定義：一類特殊的單形
定義,奇異單形,
定義
奇藝同調群(singular homology group)是對任意拓撲空間都有定義的同調群。對每個非負數q確定一個q維單純形
，稱為q維標準單形(standard simplex)，記作△q。
奇異單形
設X是一個拓撲空間，從q維標準單形
到X連續映射稱為X的q維奇異單形(singular simplex)。拓撲空間X的奇異鏈復形(singular chain complex)，記作(S(X),∂)定義如下：
①當q≥0時，(S(X,∂)的q維鏈群S𝑞(X) 是由X的q維奇異單形生成的自由交換群，即：S𝑞(X)中的元素是X的q維奇異單形的形式有限和；當q<0時，S𝑞(X)規定為平凡群；
②(S(X),∂)的邊緣同態S𝑞(X)的任一個生成元（X的q維奇異單形）上的作用像
定義為
，其中
是標準單形△𝑞的頂點集
去掉第i個頂點得到的面，
是奇異單形作為映射在該面上的限制。若將 看作從q-1維標準單形到X的連續映射，它是σ與如下頂點對應關係給出的線性映射的複合：
（1）
；
（2）
。
拓撲空間丫奇異鏈復形(S(X,∂)的同調群稱為拓撲空間X的奇異同調群。
奇異問調群對於任意拓撲空間有定義，因此，如果不作特別聲明，拓撲空間的同調群通常指的就是奇異同調群，同倫等價的拓撲空間有同構的奇界同調群。
