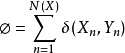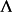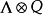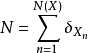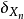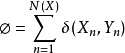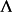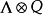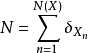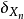考慮點過程N，對它的每一個點賦予一個輔助的隨機變數並把這個輔助變數稱作連繫於這點的標（mark），這裡的標值來自標值空間Y。把這種每一點都帶有一個標值的點過程稱作標值點過程。
基本介紹
- 中文名：標值點過程
- 外文名：marked point process
- 領域：數學
- 定義：每一點都帶有一個標值
- 屬性：點過程
- 相關名詞：自激點過程
簡介,引理,標值點過程套用,從像素到對象,統計方法,點過程,定義,套用,
簡介
定義一：
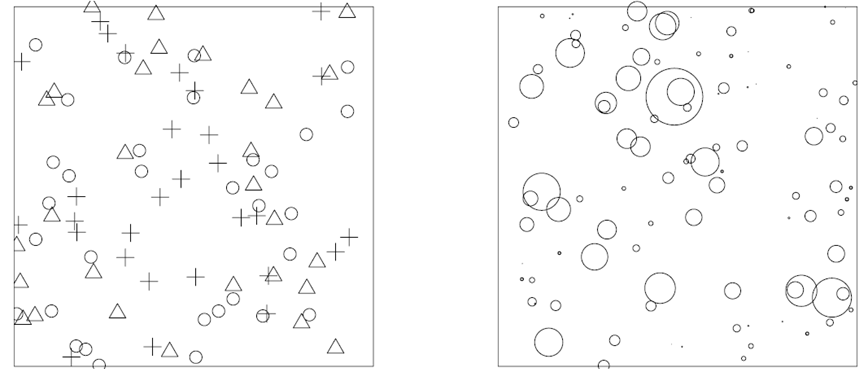
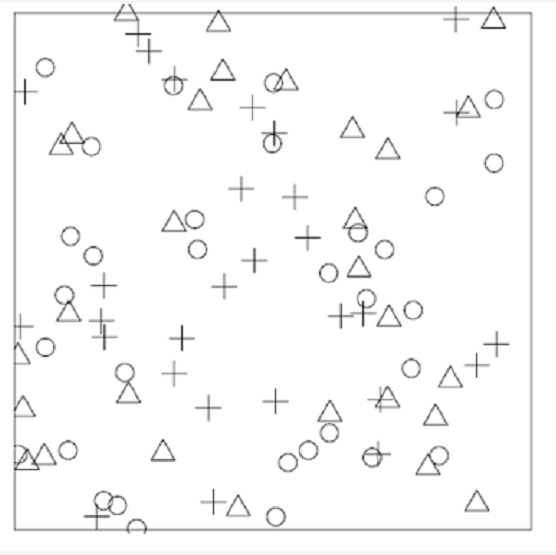
考慮點過程N，對它的每一個點賦予一個輔助的隨機變數並把這個輔助變數稱作連繫於這點的標（mark），這裡的標值來自標值空間Y。把這種每一點都帶有一個標值的點過程稱作標值點過程。
如上圖為標值點過程的示例圖，左邊：標值空間是三個離散值，△，O，+；右邊：標值空間是圓的半徑。
定義二：
假設Q是(X,Y)上的機率測度，N是X上的點過程。對於X上標值空間為Y的標值點過程我們記為φ，如果有Y1,Y2,...是Y上一系列獨立的分布為Q的隨機點，則
稱為N的Q標值點過程。
標值點過程(marked point process)一種點過程。令點過程的每一點聯繫一個標值，就得到標值點過程。設{N(t),t}是一基本的點過程，如果對這過程的每一點t (n=1,2,3,...)賦予一個輔助的隨機變數u ，並稱之為聯繫於該點的標值，變數u隨機地取值於某一標值空間au，這種每一點都帶有一個標值的點過程即稱為標值點過程。而由定義的隨機過程則稱為伴隨的標值累計過程。當標值變數u不含取值0時，標值點過程和它的標值累計過程是一一對應的，因此認為它們是等同的。
標值空間iu可以是一般的抽象空間。但是，為了能夠考慮標值的累加，通常要求在Gu中定義有“加法”運算.在一般的標值點過程定義中既不要求標值{u }是獨立隨機變數序列，也沒有規定標值要獨立於基本點過程一般的標值點過程套用範圍很廣，複合泊松過程可以看做是一類特殊的標值點過程。
引理
引理一：對於標值空間為Y的標值點過程X是一個X×Y的點過程。
引理二：若N是X上的點過程，均值強度為
，φ是N的Q標值點過程。則φ的均值強度為
。
標值點過程套用
標值點過程是一種有效的建模方法，在很多領域得到了廣泛的套用，本章將詳細介紹標值點過程理論，討論其模擬方法和最佳化算法，並給出使用標值點過程進行目標提取的基本框架。
標值點過程用於目標提取，主要有兩個優勢,一、該方法是一種面向對象的方法二、該方法是基於統計框架的。下面從這兩個方面進行介紹。
從像素到對象
傳統的道路提取的方法一般是建立在基於像素級別的光譜信息分析的基礎上，它們的共同特徵是主要使用圖像的強度量即灰度值的統汁信息，而對地物形狀、結構等信息的分析很少涉及。在高解析度圖像中，道路表現為具有一定的寬度的“面狀物”，具有豐富的細節信息，並存在較多的噪聲干擾車輛、樹木、陰影等，使用像素級方法一般很難得到較好的提取結果。面向對象的思想來源於軟體工程領域，其特點是將影像對象作為影像分析的基本單元。影像對象是指影像分割後若干“同質”像素的集合。在很多特徵信息提取的問題中，能夠完整表現目標特徵的並非單個像元，而是那些“同質”像素的集合，因此，基於對象的分析方法更符合實際情況，能更好地利用目標的特徵。採用面向對象的方法有以下優勢一、可以較好的解決噪聲問題，噪聲區域將和其周邊的像元一起合併到特定的影像對象中去二、可充分利用目標的幾何結構特徵長、寬等和光譜特徵方差、均值等三、可充分利用目標的空間特徵距離、方向等，使專家知識能直接指導圖像分析。基於標值點過程提取目標的方法是一種面向對象的方法。這種方法根據對象的幾何特徵建立模型，根據目標的光譜特性建立數據項,根據目標的拓撲性質等空間特性建立先驗項。
統計方法
標值點過程的方法克服了MRF的不足。它從對象的角度建立目標的模型，每個標值點可以表示複雜的結構，可以較好的解決噪聲問題。而且，這種方法可以通過定義標值點之間的相互關係來描述目標形狀和全局結構。
點過程
定義
描述隨機點分布的隨機過程。很多隨機現象發生的時刻、地點、狀態等往往可以用某一空間上的點來表示。例如，服務台前顧客的到來時刻，真空管陰極電子的發射時刻，可表為實軸上的點。又如，天空中某一區域內星體的分布，核醫療中放射性示蹤物質在人體器官的各處出現，不同能級地震的發生，都可用二維以上空間的點表示。點過程就是描述這類現象的理想化的數學模型。它在隨機服務系統、交通運輸、物理學和地球物理學、生態學、神經生理學、傳染病學、信息傳輸、核醫療學等很多方面都有套用。
對於X的點過程是從一個機率空間到(N,N)的一個可度量映射N。N是最小域可數子集。
其中，
是示性函式。
套用
隨機測度的收斂與極限問題相應於測度序列的各種收斂性，可以定義隨機測度（隨機點過程）的弱收斂強收斂、淡收斂、依分布收斂等（見機率論中的收斂），=。並可研究其相互關係，從而進一步研究在一定條件下隨機測度序列收斂到某個特殊隨機測度的問題。這一類問題與無窮可分點過程理論密切相關。一個有趣的結果是：相互獨立的隨機點過程的疊加，若滿足所謂一致稀疏條件，則疊加過程收斂於泊松過程。它與中心極限定理中獨立隨機變數的標準化部分和收斂於常態分配的結果相似。類似於特徵函式與母函式（見機率分布）在研究隨機變數的分布及其極限理論中的作用，對於點過程，也可以定義機率母泛函與拉普拉斯泛函，作為研究其極限問題的重要工具。
點過程與隨機幾何60年代後，由於自然科學和其他實際問題的需要，產生了大量與點、線、面等幾何元素的隨機分布有關的機率問題，它們屬於隨機幾何的範疇。例如，研究細胞核中成對染色體的相對位置，需要求出在兩同心圓上均勻分布的兩隨機點距離的機率分布，由研究聲波反射而提出的求平均路長問題等。布豐的投針問題(見機率)可能是最早的這類問題之一，它求出了隨機拋一枚針與一組等距離的平行線不相交的機率，從而可以用實驗的方法求得圓周率π的近似值。點過程及其進一步的發展還與隨機幾何相聯繫,產生了線過程、面過程、超平面過程、隨機分叉樹等模型，它們又可以經過一定的變換，變為某一個流形上的點過程。例如平面上的一條直線，它以與原點的距離及與坐標軸的交角為參數，可以對應柱面上一點，因而平面上的隨機線過程可以表為柱面上的隨機點過程。
