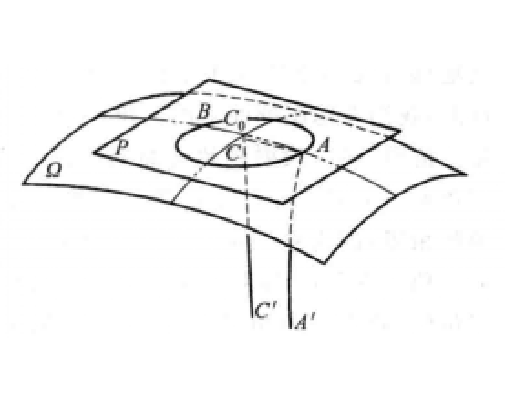
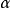極限球面(horosphere)是羅氏空間的三種基本曲面之一,指在羅氏空間中,從直線a的一個點A,到在確定方向上與a平行的任意直線引等傾割線,其端點的幾何軌跡。點A也是極限球面上的點,直線a及與a在同方向平行的直線稱為極限球面的軸線,極限球面是拋物線把的直交曲面,也是極限圓繞其任一軸線旋轉一周所產生的曲面。
基本介紹
- 中文名:極限球面
- 外文名:horosphere
- 所屬學科:數學(幾何學)
- 相關概念:羅巴切夫斯基空間,直道線等
基本介紹,定義,基本定理,極限球面上的絕對幾何學,極限球面上的弧和角,極限球面上的平行理論,
基本介紹
定義
極限球面是羅巴切夫斯基空間中的一種曲面,它是由極限圓繞其一個軸旋轉而生成的。空間中的極限球面相當於平面上的極限圓,因此,極限球面亦可以定義為一種軌跡,過直線a上某點M在一定方向上向空間中所有與該直線平行直線引斜率相等的截線,截線端點的軌跡就是一極限球面,點M叫做極限球面之球心, 直線a叫做極限球面的軸。若已知軸a及軸上一點M,則極限球面便已確定。
極限球面又叫極曲面。
基本定理
定理1 線把的C-曲面為點的軌跡,這些點都在線把內的半線上,且和線把內某一條選定的半線上某一個起點對應,線把內的半線都nU作這個C-曲面的軸。
定理3 平行線把的C-曲面叫作渾球面或叫作極限球面,它是極限圓繞著它的軸旋轉所成的曲面。
事實上,極限球面的直徑面截口上的一切點,在直徑面上一個平行半線束里的半線上互相對應,故為一個極限圓。這極限圓繞著它的軸旋轉便得極限球面。
定理4 一切極限球面全等。
定理5 經過極限球面上一點的平面,或者和它相切,或者和它相交於一圓或一極限圓。
極限球面上的絕對幾何學
我們的目的是要建立極限球面上的內在幾何學,這在敘述羅巴切夫斯基幾何學進一步的發展時,是有極重要的意義的,我們在這裡要努力使建立這種幾何學的程式,儘可能地和建立平面幾何學的程式接近,正如在平面幾何學一樣,我們首先建立基本概念和起公理作用的基本命題,然後對由這些命題所得到的推論做一概述,但我們現在既然已經知道了極限球面在空間的性質,那么,和平面幾何學不同,極限球面上的幾何學的基本概念,將不是沒有定義的名詞,而將給以定義,同樣,它的基本命題也不是公理,而是羅巴切夫斯基空間幾何學的定理。
類似地,我們引進極限球面上的幾何學的基本概念。
1) 所謂“點”是指已知極限球面上的點。
2) 所謂極限球面的“直道線”是指它的直徑面截口,即屬於已知極限球面的極限圓。
3) 如果點在極限圓上,我們說點和直道線相關聯。
4) 如果在平面ABC上,極限球面的軸BB’介於兩軸AA'和CC’之間,我們說:在直道線ABC上,點B介於點A和點C之間。
5)所謂圖形的“運動”是僅指那些運動,當運動時,圖形的各點經常保留在已知的極限球面上。
我們現在來列舉一些命題,在這裡即需指出,這些命題和平面幾何學的公理是相類似的。
1. 經過極限球面上兩個不相同的點,在這曲面上有一條且僅有一條直道線。經過極限球面的任意兩點A,B有一個且僅有一個直徑面,而極限球面上的極限圓就是它和直徑面的交線。
2. 在每條直道線上最少有兩點。
3. 有不在同一直道線上的三點存在。
4. 同一直道線上三個不同的點之中,總有且僅有一點介於其他兩點之間。
5. 設A,B為兩個不同的點.則在直道線AB上,存在著無窮多點介於A和B之間,也存在著無窮多點,使點B介於點A和它們中任何一點之間。
6. 直道線上任何點O,劃分它上面其餘的點為兩類,使點O介於任何不同類的兩點之間,但不介於同類的兩點之間。
7. 極限球面上的直道線把它劃分為兩個凸區域。
8. 極限球面上兩個運動繼續舉行的結果,也是極限球面上的運動;又極限球面上每個運動的逆運動,也是極限球面上的運動。
9. 極限球面上的運動,把直道線段變為直道線段。這是很明顯的,因為經過運動之後,極限圓仍是極限圓,在它弧上的點仍留在弧上。
10. 在極限球面上,正如在其他每個C-曲面上一樣,極限球面在其自身上有移轉的自由。
11. 存在著這樣的運動,把直道線段AB變為直道線段BA。又把這兩個直道線段的夾角AOB,變為角BOA。
12. 如果把極限球面上有向直道線上各點,劃分為兩個戴德金特的類,那么,或者在第一類里有最後的點,或者在第二類里有最前的點。
極限球面上的弧和角
套用以上所述的這些命題,我們可以建立相等的概念,那是對於極限圓的弧段和在極限球面上同過一點的兩弧所成的夾角來說的,如果兩個弧段或兩個角經過運動後彼此疊合,我們便說兩弧相等,或兩角相等。通常的辦法,我們建立補角和對頂角的概念,並把極限球面上的圓定義為自極限球面上一點出發的等長極限圓弧的終點的軌跡,我們容易見到這樣定義的“極限球面上的圓”,對於外圍空間來說,也是一個圓。事實上,設在極限球面上,給定一段極限圓弧OM,那么,把這弧在極限球面上繞著點O而轉動,它畫成一個圓,這是依照極限球面的內在幾何學的意義來說的,但點M的運動,同時也是它繞著極限球軸OO'的轉動,由於這樣的運動,它顯然也畫出一個圓。這是依照外圍空間的幾何意義來說的。
由平面幾何學中關於相等的角和全等三角形的定理,我們可以得到關於極限圓弧所作成的角和三角形的相等關係的定理。
取不相等的極限圓弧,或極限圓弧所夾的不相等的角,把一個放在另一個之上,我們也像在平面幾何學裡比較不相等的線段和角一樣,可以確定它們孰大孰小,因以得到關於不等式的定理,這和平面幾何學裡對應的定理完全類似。特別的例子有,如極限圓弧所作成的三角形,我們得到它的每邊小於其他兩邊之和的定理,由此定理又可推得:極限球面的直道線同時也是極限球面上聯結兩點的所有曲線中最短的曲線。
最後,與平面幾何學裡所建立的關於線段和角的測度理論完全相仿,我們建立極限圓弧和這些弧所夾的角的測度理論。
定理6如果每一極限圓弧段取得正數,令:1)相等的弧段取同一個數;2) 弧段的和所取的數,等於被加弧段所取的數之和,那么,對於所有的弧段,這個數等於用某個弧段單位去測量它們所得的長度。
定理7如果每一為兩個極限圓弧所夾的角,取得正數,令:1)相等角取得同一個數,2)兩角之和所取的數,等於被加角所取的數之和,那么,任何角所取的數,等於用某個定角為單位去測量它所得的角量。
這兩條定理可以用來比較在極限球面上內在幾何學裡測度的結果,和在外圍空間的幾何學裡對於同一量的測度結果。
極限圓的弧長正如其他一切曲線的弧長一樣,可以看作折線的周長的極限,其折線的每段都為直線而內接於該弧,用這方法,每段極限圓弧可用一個數表示,此數顯然適合定理1的條件1) 和2),由此推得:
如果把極限圓的弧長定義為它的內接折線的周長的極限,並令某段弧AB的長等於1,那么,在極限球面的內在幾何學裡任意另一段的弧長,等於以弧AB 為長的單位來測量該弧所得的結果。
同樣地,在外圍空間兩條曲線所成之角,便是它們在交點的切線所成的夾角,把這個角的定義施用於相交的極限圓,我們對於每個這樣的角,用一個數來代表,這個數適合定理2的條件1) 和2),由此推得:
如果把兩個相交極限圓弧OA,OB 的切線的夾角取為角的單位,那么,在極限球面的內在幾何學裡,用兩弧OA,OB 的夾角AOB 為單位,來量任何其他兩個極限圓弧的夾角所得的結果,和它們的切線的夾角相同。換句話說,在極限球面的內在幾何學裡,兩個極限圓的夾角,便是在它們交點和極限圓相切的兩條直線所夾的角。
極限球面上的平行理論
13. 經過極限球面上不屬於直道線CD的點A,只能作一條直道線AP,直道線CD不相交。
和平行公理比較,我們可見在極限球面的內在幾何學裡,這條基本命題,可從歐幾里得幾何學的平行公理得來,如果把這公理的“直線”這個名詞改為“直道線”,把“平面”改為“極限球面”的話。
現在檢閱極限球面的內在幾何學中所有13條基本命題,它們都可由歐幾里得平面幾何學公理得來,只需把“直線”這個名詞改為“直道線”,把“平面”改為“極限球面”便成,因此,歐幾里得平面幾何學中所有的定理,在極限球面的內在幾何學中依然成立,只需把其中的“直線”改為“直道線”,把其中的“平面”改 為“ 極限球面”。
換句話說,極限球面的內在幾何學和歐幾里得平面幾何學的差別,只在兩個基本概念有不同的名稱。
這個著名的事實也是羅巴切夫斯基本人所發現的,並且對於非歐幾里得幾何學的建立,起了很重要的作用,這首先表示:如果根據任何理由,通使我們認為歐幾里得公設對於平面幾何學是不正確的,那么,這並非意味著歐幾里得所建立的幾何學失去了它的意義,它依然可以成立,不過不是在平面上,而是在極限球面上。
利用歐幾里得公理系統現成的結果,我們得到一系列的事實,這些事實不但對於極限球面的研究是重要的,而且對於所有有關羅巴切夫斯基空間的研究,也同樣重要。
從這些事實中我們提出下面幾條:
1. 在極限球面上三個極限圓弧所圍成的三角形,它的各內角之和等於兩直角。
2.在極限球面上分別為極限圓弧所圍成的兩個三角形,稱為彼此相似,如果它們的對應角相等,對應邊成比例。
我們可以斷定,在極限球面上,有彼此相似同時不相等的三角形存在,因為對於歐兒里得平面上的直線三角形,相對應的結果是成立的。
3.在極限球面上,組成三角形的極限圓的弧長與角間的關係,和在歐幾里得平面上直線:三角形的邊與角的關係相同。換句話說,歐幾里得平面三角形中所有的關係式對於極限球面上的弧三角形都成立。
4.設在平面P 上給定一個圓,點C為圓心,CA 為半徑(圓1),在點C作平面P的垂線CC'。過圓上點A作直線AA'和半線CC'平行,又在半線CC' 的延長線上求得點A 的對應點C0。在平面CC'A' 上,經過點C0,且以CC' 為軸的極限圓,應當經過圓周上的點A,因為點A 和點C0是對應點,再把這極限圓繞著軸CC'旋轉,我們得到一個極限球面Ω,而所給的圓在這球面上,並且它在極限球面上的圓心為點C0,半徑為極限圓弧C0A。
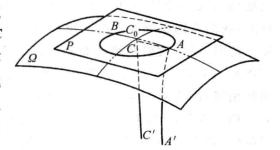 圖1
圖1因此,每個圓都在某個極限球面上,且具有完全確定的極限圓弧半徑。套用歐幾里得幾何學的相當定理,我們得到下面的結果:對於一切的圓,圓周的長度和它的極限圓弧直徑的長度的比值是一個常數。我們熟知這個比值,用字母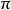 來表示的,是一個無理數,它約等於3.1416。
來表示的,是一個無理數,它約等於3.1416。
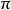
在羅巴切夫斯基幾何學裡所謂角的絕對量,是指以所給的角為圓心角時,圓弧的長度和這圓的極限圓弧半徑的長度的比值。因為圓周的長 ,那么,角的絕對量
,那么,角的絕對量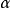 和它的角度
和它的角度 的關係,可表以通常公式
的關係,可表以通常公式