基本介紹
- 中文名：極小弦
- 外文名：minimal chord
- 所屬學科：數學
- 所屬問題：平面幾何（圓）
- 定義：指過圓內一點的最短弦
基本概念,關於弦的定理,點對圓的冪,
基本概念
過圓內一定點的所有弦，以被此點平分者為最短(圖1)。
被圓內某點平分的弦，叫做過該點的極小弦。
圖1關於弦的定理
定理1 在一圓中(圖2):
(1)垂直於弦的直徑必平分此弦及其所對的弧；
(2)平分非直徑的弦的直徑必垂直於此弦；
(3)平分弦的直徑必垂直於此弧所對的弦。
圖2定理2 在同圓或等圓中(圖3)：
(1)等弦對等圓心角，較大的弦對較大的圓心角；
(2)等圓心角夾等弦，較大的圓心角夾較大的弦。
圖3定理3 在同圓或等圓中(圖4):
(1)等弦對等弧，較大的弦對較大的弧；
(2)等弧對等弦，較大的弧對較大的弦。
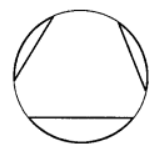圖4定理4 在一圓中，直徑是最大的弦。
定理5 在同圓或等圓中(圖5)：
(1)等弦距圓心等遠，較大的弦距圓心較近；
(2)距圓心等遠的弦等長，距圓心較近的弦較大。
圖5點對圓的冪
點對圓的冪(power of a point with respect to a circle)亦稱點對圓的方冪，是一個實常數，即過一定點對圓任作一條割線，交該圓於兩點，自定點至兩交點的兩條有向線段的積(線段同向時積為正，線段異向時積為負)是一個實常數，此常數稱為定點對於該圓的冪，簡稱圓冪。在此意義下“冪”這個詞是德國著名數學家施泰納(Steiner，J.)首先使用的。設P點為定點，⊙O為定圓，半徑為r，則
(常數)，k就是P點對於⊙O的冪，當P點在⊙O的外部時(如圖6)，k值為正，這時k=PC，其中PC是P點到⊙O的切線的長；當P點在⊙O內部時(如圖7)，k值為負，它的絕對值等於過P點的極小弦EF的一半的平方；當P點在⊙O上時，k的值為零。無論何種情況，k的值都可以表示為k=PO-r。
圖6
圖7