棋盤多項式

棋盤多項式是組合數學中一種用於解決有限制排列問題的方法理論。

基本介紹

• 中文名：棋盤多項式 
• 外文名：Rook polynomial

定義

設C為一棋盤，稱

為C的棋盤多項式，其中 表示k個棋子布到棋盤C的方案數，要求同一行（列）至多有一個棋子。

原理

n個不同元素的一個全排列可看做n個相同的棋子在n×n的棋盤上的一個布局。布局滿足同一行（列）中有且僅有一個棋子。如右圖所示的布局對應於排列41352。

可以把棋盤的形狀推廣到任意形狀，對於棋盤C，令 表示k個棋子布到棋盤C上的方案數。下圖中給出了幾個例子。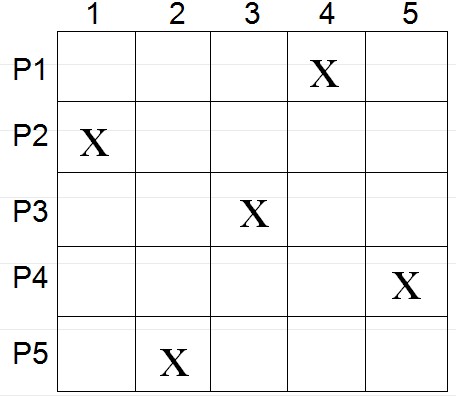

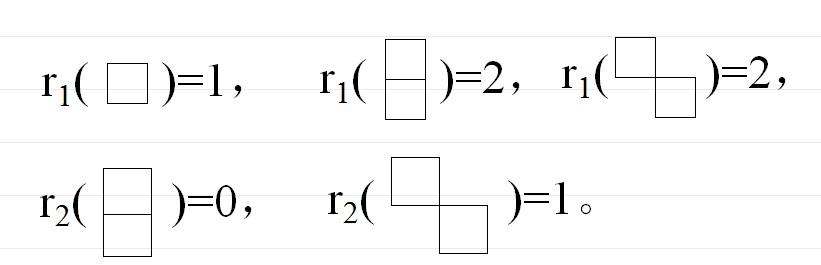rk(C)舉例

則定義

為棋盤C的棋盤多項式，假定棋盤C可布n個棋子，但不能超過n個，其中規定 。

特性

性質1：設是棋盤C的某一指定格子所在的行與列都去掉後所得的棋盤；是僅去掉該格子後的棋盤。

則： （1）

與之對應，有： （2）

推導：對於棋盤C某一格子僅有兩種可能：一種是該格子上有棋子，另一種即該格子上未放置棋子，由此則可得出公式（1）中的兩項。

性質2：如果C由相互分離的C1，C2組成，即C1的任一格子所在的行和列中都沒有C2的格子。

則：

此時：

套用

有禁區的排列

設 為 i個棋子布入禁區的方案數，i =1,2,3,…,n。則有禁區的布子方案數（即禁區內不布棋子的方案數）為

舉例

例：1、2、3、4四位工人，A，B，C，D四項任務。1不乾B；2不乾B、C;3不乾C、D；4不乾D。問有多少種可行方案？

解：棋盤圖案如右圖，其中陰影部分表示禁區，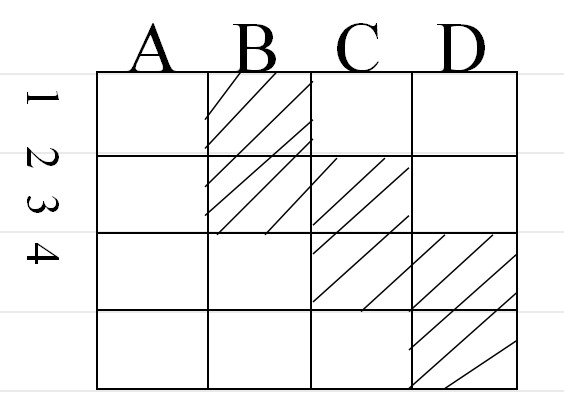

根據棋盤多項式性質，可得陰影部分棋盤多項式為：

根據有禁區排列公式，得：

方案數=4!－6(4－1)!+10(4－2)!－4(4－3)!+0(4－4)!=4