梯形蝴蝶定理

梯形蝴蝶定理是指平面幾何中的重要定理，由於該定理的幾何圖形形象奇特，形似蝴蝶，所以以蝴蝶來命名。計算公式有S3: S4=ab：cd。

基本介紹

• 中文名：梯形蝴蝶定理
• 屬於：平面幾何中的重要定理
• 名稱來由：定理的幾何圖形形似蝴蝶
• 公式：S3: S4=ab：cd等

定理

如圖，在梯形中，存在以下關係：

1. 相似圖形，面積比等於對邊比的平方也就是S1：S2=a^2/b^2
   
2. S1:S2:S3:S4= a2:b2:ab:ab
   
3. S3=S4
   
4. S1×S2=S3×S4(由S1/S3=S4/S2推導出)
   
5. AO:BO=(S1+S3):(S2+S4)
   

證明

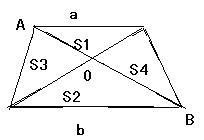
左上角為A，右下角為B

S1和S2的的三角形是相似的,所以面積比=邊長比的平方即a²：b² 設梯形高為h，S3+S2=1/2 bh=S4+S2.所以S3=S4 設S4三角形高為h1（底為OB），可知S3:S1=S4：S1=OB:OA 。因為S1和S2的的三角形是相似，S4:S1=OB:OA=b：a 所以S1︰S2︰S3︰S4= a^2︰b^2︰ab︰ab