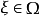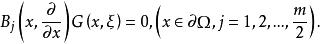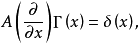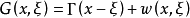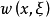格林運算元(Green's operator)是微分p形式空間到調和p形式空間的直交補的一個映射。設G:Ep(M)→(Hp)⊥,ᗄα∈Ep(M),G(α)是方程Δω=α-H(α)在(Hp)⊥中的惟一解,其中H:Ep(M)→Hp是一個投影運算元,就稱G為一個格林運算元。
基本介紹
- 中文名:格林運算元
- 外文名:Green's operator
- 所屬學科:數學
- 所屬領域:偏微分方程
定義,格林運算元的性質,相關解釋,高階橢圓型方程的格林運算元,
定義
格林運算元(Green's operator)是微分p形式空間到調和p形式空間的直交補的一個映射。設 是方程
是方程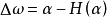 在
在 中的惟一解,其中
中的惟一解,其中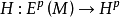 是一個投影運算元,就稱
是一個投影運算元,就稱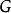 為一個格林運算元。
為一個格林運算元。

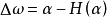

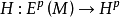
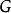
格林運算元的性質
運算元G的性質:
1.G是一個有界自伴隨線性運算元;
2.把有界序列變成有柯西子序列的序列;
利用格林運算元易得到:
2.定向緊微分流形的德拉姆上同調群都是有限維的。
相關解釋
格林運算元(Green operator)即二階橢圓運算元的逆運算元,考慮二階橢圓型方程
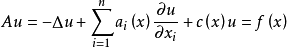

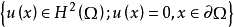
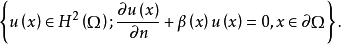

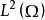
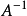
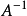
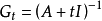

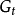
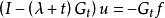
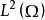
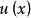
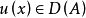
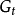
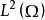
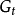
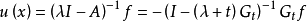
高階橢圓型方程的格林運算元
高階橢圓運算元的格林運算元(Green operator of higher order elliptic equation)的構造,對於高階橢圓型方程的一般邊值問題
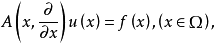
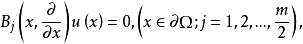
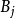
1.在∂Ω的一切點x處,∂Ω的法線方向不是任何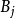 的特徵方向;
的特徵方向;
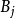
2.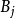 的階
的階 並且
並且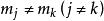 ;
;
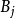

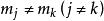
A的定義域是
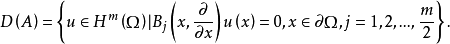
當A是 到
到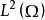 上的一一映射時,
上的一一映射時,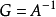 稱為上述問題的格林運算元。如果A與x無關,且設Γ(x)是它的基本解,即
稱為上述問題的格林運算元。如果A與x無關,且設Γ(x)是它的基本解,即

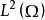
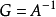
1.對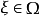 ,
,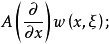
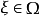
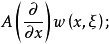
2.對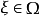 ,
,