格才高爾契克分層是格才高爾契克(Grzegor-czyk, A.)於1953年引進的對原始遞歸函式類的一種分層。
基本介紹
- 中文名:格才高爾契克分層
- 外文名:Grzegorczyk hierarchy
格才高爾契克分層(Grzegorczyk hierarchy)遞歸論的基本概念之一簡稱“格氏分層”或“G分層”.格氏首先定義了下列函式列(稱為“格才高爾契克函式列”):
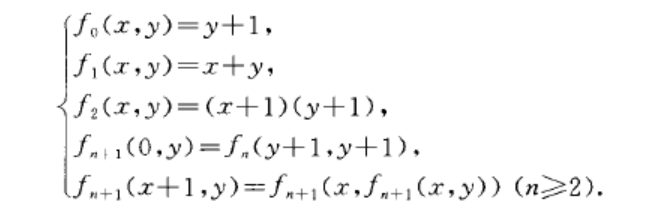
格才高爾契克函式列
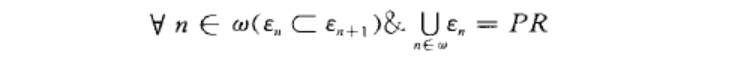
格才高爾契克分層
(PR表示全體原始遞歸函式類),即。。。。。構成PR的一個不塌方的分層.1963年,里奇(Ritchie, R.W.)證明了ennE。定義中的格氏函式列可以改用下列更自然的阿克曼型函式列:
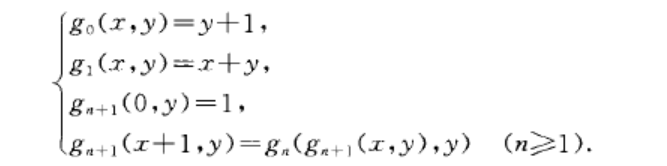
格才高爾契克分層
在G分層中,e3恰好是初等函式類.而E。則是相當簡單的函式類,它以lx y(二+y)為控制函式.但是,格氏證明了任何遞歸函式f都可表成下列範式:.(f<xl,xz,…,x‑)=(ACyBCx,x‑xz,…x)=(0),其中A,BEEo.此外,律庭(Rodding , D.)和馬琴科夫(Marchenkov,S. S.)分別於1964年和1969年證明了。‑(n,3)和。:都是複合集,即可由有限個開始函式經複合運算而生成.但。。,。,是否也是複合集則尚不可知.若以C‘表示函式類C中的(0,1)值函式之集,則(En )nE。是一個十分有意義的函式類序列.據格才高爾契克與里奇的工作,對任何n,2,有E‑C E,幾1·但Eo CE74 CE2之包含關係是否也是嚴格的則尚不清楚.由於Ep與圖靈機線上性空間內所接受的關係類LISPACE相同.因此,上述問題亦是計算複雜性理論中的一個重要的未解決問題.另外,G分層還有許多形式的延伸,它們構成某個真擴張原始遞歸函式類的函式類的一種分層.
