柯西初值問題

柯西初值問題（Cauchy initial value problem）是微分方程的一種基本定解問題。

基本介紹

• 中文名：柯西初值問題
• 外文名：Cauchy initial value problem
• 適用範圍：數理科學

簡介

柯西初值問題是微分方程的一種基本定解問題。

微分方程的解

設f(z,ω)是定義在復空間C×Cⁿ的一個區域Ω⊂C×Cⁿ上的復變數向量解析函式，則可考慮微分方程

寫成分量形式為

又設H是平面C上的一個區域，則一個解析映射w:H⊂C→Cⁿ稱為是微分方程的一個解，若它滿足下面諸式：

1、；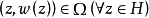

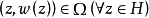
2、。

定義

下列問題稱為柯西初值問題：給出複平面C上一個區域H，區域Ω上的任一點(z₀,w₀)和一個H上的解w=w(z)，滿足w(z₀)=w₀。

上述問題又可寫成

微分方程

微分方程指含有未知函式及其導數的關係式。解微分方程就是找出未知函式。

微分方程是伴隨著微積分學一起發展起來的。微積分學的奠基人Newton和Leibniz的著作中都處理過與微分方程有關的問題。微分方程的套用十分廣泛，可以解決許多與導數有關的問題。物理中許多涉及變力的運動學、動力學問題，如空氣的阻力為速度函式的落體運動等問題，很多可以用微分方程求解。此外，微分方程在化學、工程學、經濟學和人口統計等領域都有套用。