柯塞爾原子模型

柯塞爾原子模型指的是1916年柯塞爾提出了多電子原子中的電子分布主殼層模型，即主量子數相同的電子處於同一主殼層中。對應於n=1，2，3，4，…的主殼層分別用K，L，M，N，…來表示。在同一主殼層中，不同的軌道角量子數l又分成幾個不同的分殼層，常用s，p，d，f，…表示l=0,1,2,3,…的各種轉動態。

電子數公式

下面根據泡利原理和能量最小原理計算每個主殼層中最多可容納的電子數目。對於一個確定的n，l 可取0，1，2，…(n－1)共n個值，對於一個確定的l可以有(2l+1)不同的ml，對每個ml ，又有兩個ms 。根據泡利原理，可以算出原子中具有相同主量子數n的電子數目最多為

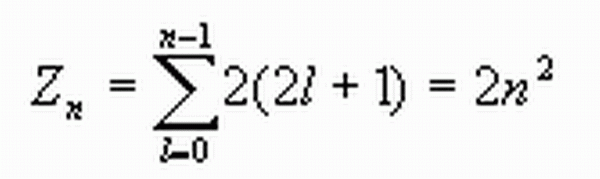電子數公式

當n=1，l =0時K殼層上可能有2個電子，這個組態用1s表示，1s是光譜學符號。當n=2，l =0時（L殼層，s分殼層），可能有兩個電子，組態以2s表示；當n=2，l =1時（L殼層，p分殼層），可能有6個子，組態以2p表示。

最多電子數

下表列出了原子內各主殼層和分殼層上可容納的最多電子數。

L; N	0; (s)	1; (p)	2; (d)	3; (f)	4; (g)	5; (h)	6; (i)	Zn
1(K)	2(1s)							2
2(L)	2(2s)	6(2p)						8
3(M)	2(3s)	6(3p)	10(3d)					18
4(N)	2(4s)	6(4p)	10(4d)	14(4f)				32
5(O)	2(5s)	6(5p)	10(5d)	14(5f)	18(5g)			50
6(P)	2(6s)	6(6p)	10(6d)	14(6f)	18(6g)	22(6h)		72
7(Q)	2(7s)	6(7p)	10(7d)	14(7f)	18(7g)	22(7h)	26(7i)	98

實際差異

1869年門捷列夫根據元素的物理性質和化學性質將它們組織到元素周期表中，元素周期表中一百多種元素排成7個周期，每個周期的元素個數依次為2、8、8、18、18、32、32，同上表中每個主殼層可容納的電子數並不完全吻合。這是因為能級不完全由主量子數n決定，也與角量子數l也有關。按照能量最小原理，電子按能級的高低從低到高占據原子中的各個能級。

我國科學家徐光憲總結出的規律為：能級高低以(n+0.7l)值來確定，該值越大，能級越高。例如4s和3d兩個狀態，4s的(n+0.7l)=4，3d的(n+0.7l)=4.4，所以4s能級低於3d能級，這樣，4s態應比3d態先為電子占有。下圖畫出了各能級的高低。

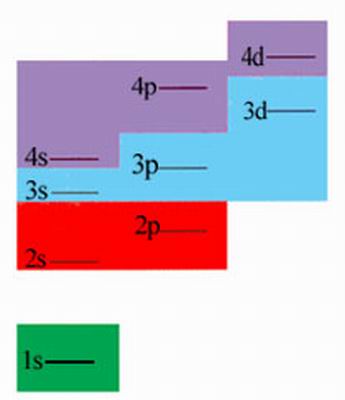
由此可得到所有元素的電子組態，即電子的殼層結構，如下圖所示，它能很好地說明元素周期表中各個周期的形成。

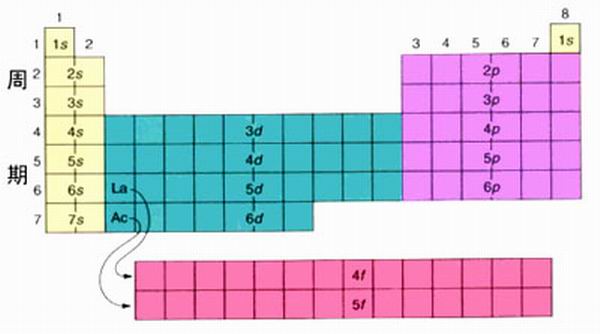
相關理論

泡利原理

1925年泡利為了解釋多電子原子的光譜規律，提出泡利不相容原理，簡稱泡利原理：

在一個原子系統內，不可能有兩個或兩個以上的電子具有相同的狀態，亦即不可能具有相同的四個量子數n, l, ml, ms 。

後來發現，凡是自旋為1/2或其它半整數的粒子都遵循泡利原理，這類粒子稱為費密子，例如電子、質子和中子都是費密子。還有一些粒子的自旋為整數，則不受泡利原理的約束，這一類粒子稱為玻色子，例如光子、介子等。

能量最小原理

能量最小原理是物理學中的普遍原理:原子系統處於正常狀態時，每個電子趨向占有最低的能級。即能量最小原理。